Guest Post by Hagen Blix and Adina Williams
Two grammars are weakly equivalent if they generate the same set of strings. If they also assign the same structural descriptions to the strings, they are also strongly equivalent. While weak equivalence may be mathematically of interest, most syntacticians, it turns out, don’t care much whether two grammars are weakly equivalent. Before we get into the thick of why that is, let us remove these notions of weak/strong equivalence from language/grammar (somehow a very contentious arena), and think about a parallelism with, say, the movement of celestial bodies (an arena where nobody never quarreled ever, so safe travels!). We won’t have any news on the linguistics front today, but if you’re a linguist, we hope you enjoy the analogy!
Let’s start at not quite the beginning. Contra to modern myth, people never really used to think that the earth was flat: There’s a horizon, it moves alongside you when you travel, the earth is, if not a sphere, at least quite definitely curved – that’s the basic empirical data, and no serious theory has ever been argued to account for it in any way but curvature. (And, to our knowledge, nobody has ever actually reached the horizon to instead prove the earth flat either.)
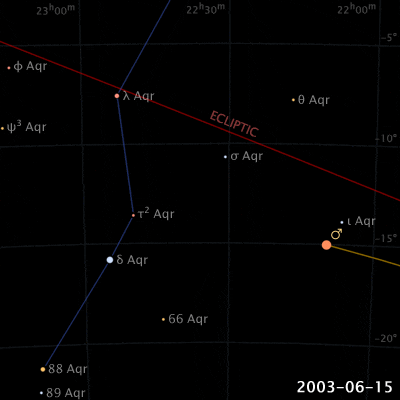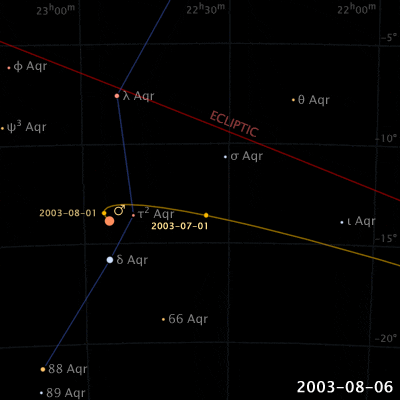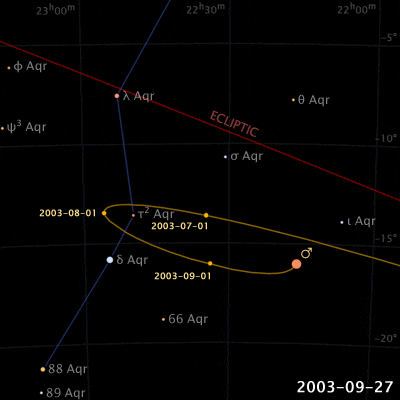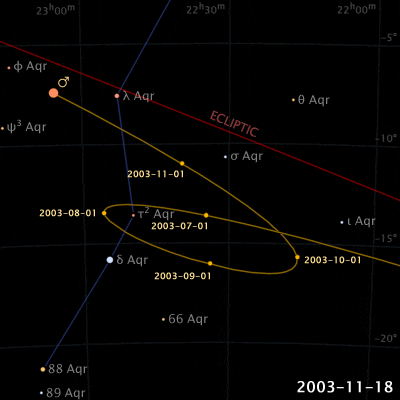
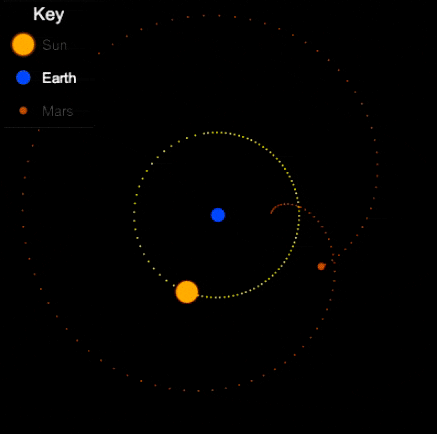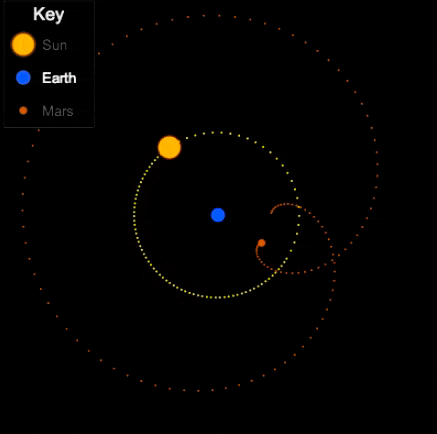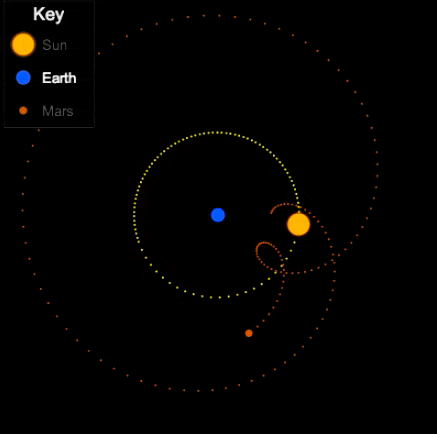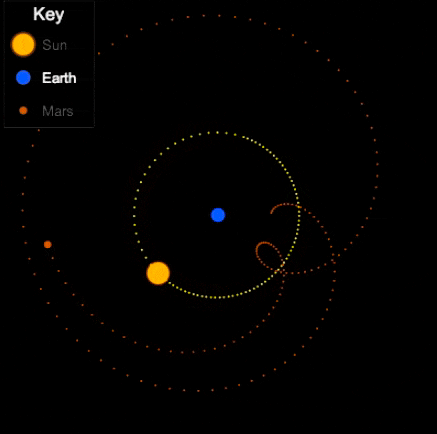
Things are different with theories of celestial motion, where people definitely disagreed. The basic empirical data concerns how bright spots move across the sky. First of all, there is the sun, moving east to west every day. But also the moon, and lots of other bright little spots. Most of those move together, but some take their own curious paths: Jupiter, Mars, Venus, and their ilk (see the path of Venus below). For example, bodies like Mars sometimes move in a kind of back-and-forth swipe across the sky (given a fixed vantage point on Earth), called retrograde, see the animation below. For theories of celestial motion, that’s the basic kind of data we want our models to capture: Paths that spots take across the sky.
Our current theories for capturing this basic data derive the easily observable (paths that bright spots take across the sky) from the much harder to observe (bodies pulling each other around out there in space). These days, we capture this data with a heliocentric model (sun in center), and planets on elliptical orbits around it. The movement of the bright dots is more or less a projection from the actual 3D movement in space onto the 2D-ish sky. Maybe we were taught in middle school that people used to believe that the earth was at the center (geocentric models), just because they saw the sun move across the sky, and because humans are all a bit narcissistic.
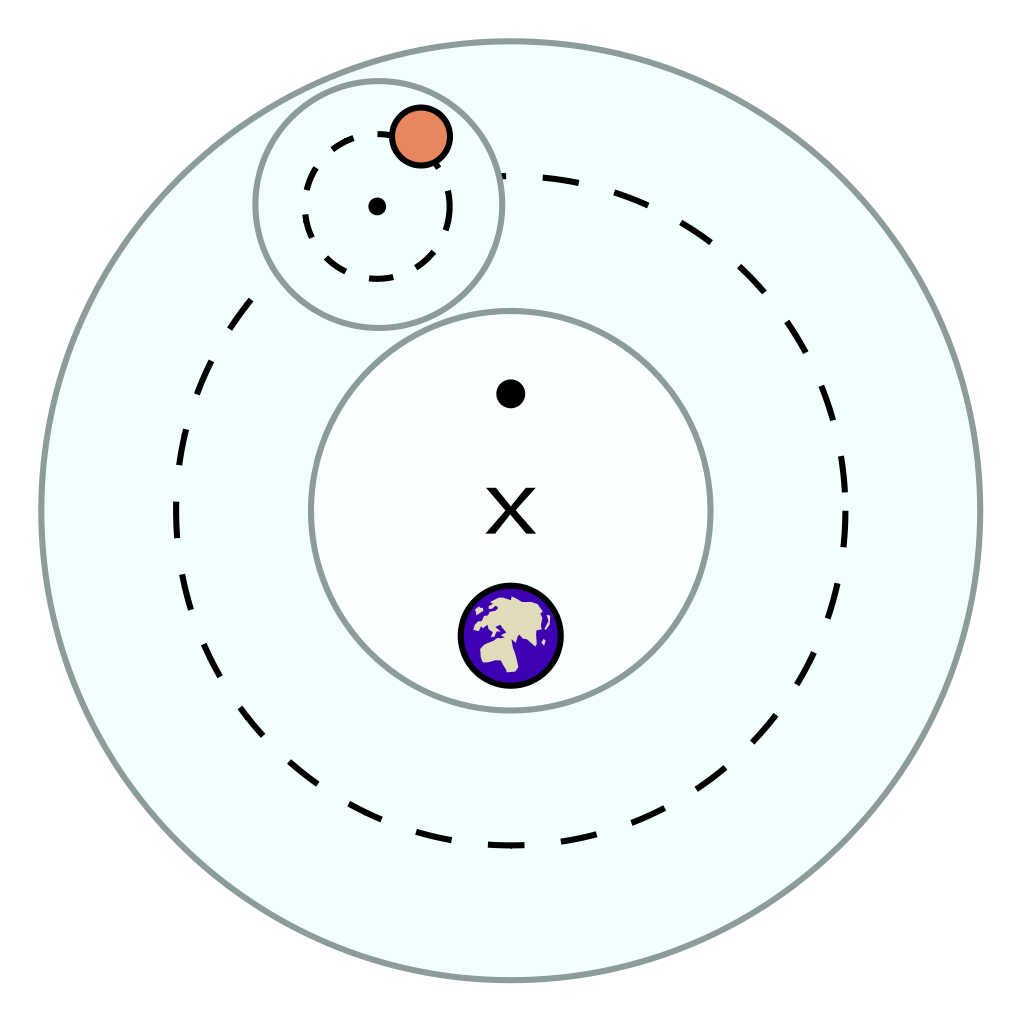
Now, if that’s the degree of familiarity you have with the history of astronomy, it may come as a surprise to you that the ancient geocentric model of Ptolemy (c. 100-170) is both sophisticated, and quite good at actually describing/predicting those paths. The key aspects are: a) an earth that is slightly off-center, and b) the possibility for bodies like Venus and Mars to move not in a circle, but in an epicycle: A small circular motion around the circle (see Mars’ looping orbit in the gif below).
Epicycles derive facts about the path of bright spots in the sky – we can see Mars in retrograde in the animation above: Effectively, the hypothesis is that Mars doesn’t directly orbit Earth, it actually orbits a point that orbits Earth, i.e., two circular movements. Sometimes the sum of these two movement cycles will mean Mars goes “backwards”, and thus the sum of two simple aspects (circular movement) gives us the complex facts about a loopy movement path in the sky.
Anyways – if you want to learn more about the actual history of astronomy (as opposed to the weird middle school version we all had to learn), we recommend this series of blog posts by scifi author Michael Flynn (there might be the occasional quarrel after all, whoops!). What’s important for us here, is that the heliocentric models that we all learn about now… weren’t really any better at accounting for those paths of little (or big) bright spots in the sky than their geocentric Ptolemaic competition. As far as the immediately observable data was concerned, the models were, well, pretty much equivalent. One might even say they were the astronomy version of “weakly equivalent”.
Why do we now scoff at geocentric theories and believe heliocentric ones when they both adequately captured the observed paths of celestial bodies? What changed the game? The answer is a new kind of data: the phases of Venus. While both geocentric and heliocentric theories could account for the original data about the paths of bright spots, it turns out that only the heliocentric theories could account for the crescent shapes of those bright spots.
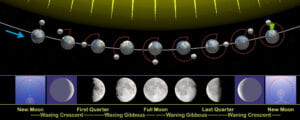
Well, everyone knew the moon had phases. It’s pretty obvious, even to us moderns, that the moon waxes and wanes. When better telescopes arrived, people took a closer look at some of those moving bright spots, and found out that other celestial bodies also have phases. Essentially, phases arise from the relative positions of three bodies: The earth (the vantage point), the sun (the light source), and the third body (the moon, Venus, etc): Only one side of a celestial body gets sunshine at any given moment (it’s “day time” over there), but that’s not necessarily the same part that is facing our way. Instead, we might see some part of the body where it’s day, and some part where it’s night. (The same is true the other way around, of course – check out the phases of the earth from the moon, though I guess they couldn’t see that stuff back then). The following figure shows how this works (in a heliocentric model) to make the moon wax and wane.
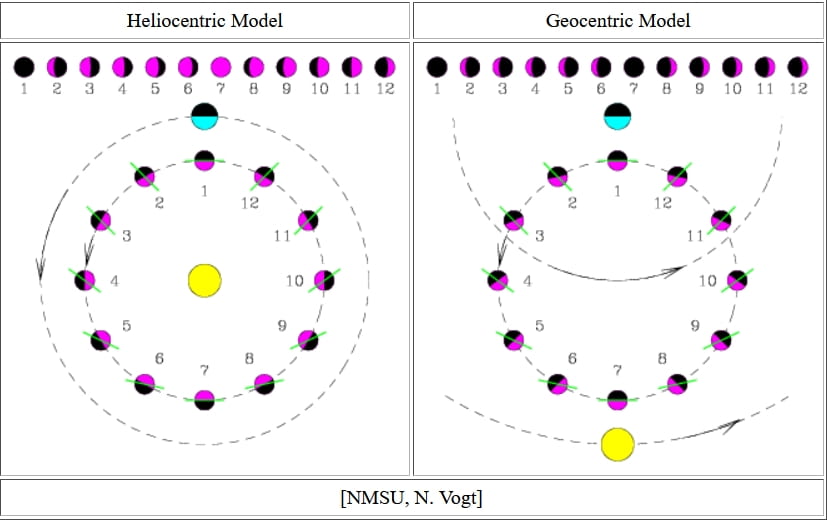
Both models apparently did pretty well for the moon in this regard. But for Venus, they made completely different predictions (see below). Both geocentric and heliocentric models postulated an “underlying structure” for space that could not be observed directly (no artificial satellites that could take pictures of a pale blue dot yet, the only perspective anybody had was that from earth). The structures of space that these models postulated were abstractions, useful in deriving the observable data: We could observe the angle between the sun and Venus in the sky, but not their actual distances from Earth (since the depth information is lost in projection – recall that our observations are 2-dimensional, but both geocentric and heliocentric models are 3-dimensional).
Now, once the movement paths were stipulated in a way that could account for the initial observations (movement of spots across the sky), one could predict the relative positions of the sun, Earth, and Venus. Hence, one could calculate the angle between the daylight area of Venus, and the area that was facing earth: The models predicted different phases of Venus to correlate with different movements of the bright spot with that name across the sky.
If you want to see an animated version, there’s a lovely visualization for each model right here:
Venus Phases in the Heliocentric Model
Venus Phases in the Ptolemaic Geocentric Model
To sum up, before we finally return to linguistics: Both models made assumptions about the way bodies move in the heavens (unobservable at the time). Both models could derive the movements of bodies in the sky (observable) as a projection from one onto the other. Both models also made predictions about the phases of celestial bodies, again based on the same assumptions about orbits. But only for one model were these predictions actually in line with the newly observable data, the phases of Venus. This was the new kind of data that made the heliocentric models win out (there’s more stuff, but this isn’t an astronomy post… arguably). Of course, centuries later, we actually launched artificial satellites, thus giving us “3D vision in the heavens”, which allowed us to more directly observe the formerly unobservable movements, but even before that, the set of abstractions from one theory did better than the other.
Now, we may say that two models for the movement of celestial bodies are weakly equivalent if they generate the same movement of bright spots across the sky (2D). But only if they were to also assign them the same movement in the heavens (3D) would we call them strongly equivalent. Astronomers, it turns out, did not care whether geocentric models are weakly equivalent to heliocentric ones. They cared about which one covered the larger range of relevant phenomena.
This means that equivalency (weak or strong) can only be understood as relative to a particular collection of phenomena (i.e., relative to the data that the theory is here to explain). In short, it is scientifically ridiculous to focus on the fact that geocentric theories are weakly equivalent to heliocentric ones relative to predicting the paths of bright spots across the sky. Clearly, that’s not the only desideratum, and it is rather blinkered to get stuck worrying about only one particular type of data. The astronomers of the day knew this, even though nobody could directly observe any movement in the heavens – at that point a purely theoretical, abstract postulate.
Syntacticians are, unfortunately, in a position reminiscent of the one that 16th century astronomers found themselves in (possibly worse, but probably with less persecution): Just as astronomers postulated unobservable movement in the heavens to explain observable movement in the sky, syntacticians postulate unobservable phrasal nodes (say, a verb phrase in English) to account for the things we directly observe: Strings such as “Jo kicked the prof” or “Mary had them eat a cake” and their associated meanings. To a syntactician, strings are a little like the bright spots moving across the sky: They are the most immediately observable phenomenon we have. We certainly want to explain them. Like the astronomers, though, we too keep uncovering new phenomena, and we definitely care about whether our previous unobservables (our abstract postulates, our structure of phrasal nodes) can account for all of them. Back to weak equivalence: Two models are weakly equivalent (relative to strings) if they generate the same set of them, even when they do so with different structures. For the purpose of this particular empirical domain – the set of possible strings – two models may well be indistinguishable. As with astronomy, the real test is whether phrasal nodes (the abstract objects that we use to derive our strings) are also useful for other kinds of data. The answer is obviously yes. Just like astronomers don’t just work only on the movement of bright spots in the sky anymore, syntacticians aren’t just (or even primarily) concerned with strings. In what follows, we will highlight some additional kinds of data that syntacticians care about, and show that all of them can be (at least mostly) handled using the abstractions that can also derive strings.
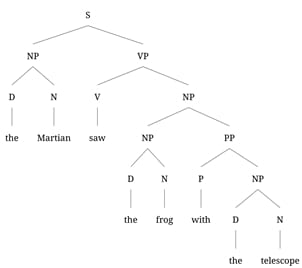
For instance, we know full well that a single string can actually correspond to multiple meanings. Take the standard example from day 1 of a Ling 101 class in (1), which exhibits a classic ambiguity:
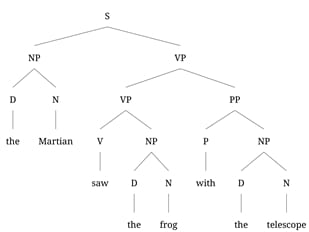
(1) The Martian saw the frog with the telescope.
Either the Martian has the telescope, and uses it to see the frog, or the frog has the telescope, and the Martian sees that frog. That such ambiguities exist is relevant to linguists in exactly the same way that the phases of Venus were to astronomers: We want them to follow from the same abstract syntactic structure that we used to generate the string. We generally introduce this idea to new linguistics students with toy phrase structure grammars like the one in (2):
This grammar has two ways of producing the string in (1), namely those in (3):
By hypothesis, these two parses correspond to the two meanings: The PP modifies either the seeing event, as an instrument, in which case it is the sister of VP. Or it modifies the frog, in which case it is the sister of NP.
Why do linguists think some hypothesis along these lines is on the right track? Because the NP nodes – our “orbits”, which we cannot observe directly – not only give us the two meanings, but they also let us account for a host of other properties. Take instance, passive sentences. We might describe some aspect of the relation between an active and a passive sentence by saying that the NP that is the sister of the verb in the active sentence is the subject of the sentence in the passive (or, in our analysis, the sister of VP), and the subject of the active sentence is the argument of a by PP in the passive. Now, in one case, the object is the frog, and in the other it is the frog with the telescope. So, if we make a passive sentence out of the active sentences above, we expect them to be disambiguated, because the two structures do no longer map onto the same string. In particular, (4b) does not have the reading where the telescope is used for seeing the frog.
The grammar in (2) allows us to capture this ambiguity and its disappearance under passivization. In entirely parallel fashion, we could look at another property associated with the NP node: Pronominalization. Maximal NP nodes can be replaced by pronouns such as they, it, she, he. Now, let’s take a look at (5), in which we “pronominalized” the NP ‘the frog’ from (3a). Again, the ambiguity disappears. This fact follows from the particular phrase structures we used to generate the string and not from the string itself.
(5) The Martian saw it with the telescope.
If the phrasal nodes are like the orbits, then structural ambiguities, passivization and pronominalization are like the phases of Venus: Properties that should follow from the same assumptions that generated the strings.
Now, let’s take an alternative grammar G’ that lacks the clause (2-b-v), the verb phrase modification VP -> VP PP. Such a grammar is weakly equivalent to G; both grammars generate exactly the same set of strings, which we can characterize as in (6).
(6) D N (PP*) V D N (PP*)
Despite their weak equivalence, linguists will obviously reject G’ in favor of G. Just as the heliocentric and the geocentric models couldn’t be distinguished solely on the basis of the movement in the sky, G and G’ cannot be distinguished solely on the basis of the set of strings they characterize. But just like the geocentric model failed to offer an adequate account of the phases of Venus, G’ fails to offer an account of the ambiguity we observed – it lacks the ability to generate two different structures corresponding to a single string. It doesn’t make the right nodes, the right structural relations available to account for all the other phenomena linguists care about. Here’s a list (highly abridged) of some other aspects of grammar that syntacticians worry about, and all of them have been argued to depend on structural relations that the phrase structure makes available.
- Scope: A girl saw every cat. (is there one girl or more than one?)
- Binding: Maryi said that shei/j came.
- Agreement: The girls from the story are/*is generating phrase structures.
- Case: He/*him came. (maybe could do a string-based theory for English, but not for more complicated case languages – see Marantz 1991, Baker 2015)
- Islands for movement: That John went home is likely v. *Who is that ___ went home likely? (Ross 1967 p.86)
- Ellipsis licensing: Valentine is a good volleyball player and I heard a rumor that Alexander is [a good volleyball player] too. v. *Valentine is a better volleyball player than I heard a rumor that Alexander is [a good volleyball player] too. Stolen from Max Papillon’s tweet
- Long Distance dependencies like “if…then”, “either…or” (Chomsky ‘57 p 22)
(See also section 2 of Adger & Svenonius 2015, they make a related point with related examples.)
In conclusion, what we really care about is whether an abstraction such as phrase structure can tie together these various phenomena. It’s for this reason that we care (a lot) about all those non-terminal nodes that, say, a phrase structure grammar generates. The ones that weak equivalence doesn’t pertain to. The pesky theoretical abstractions that aren’t (directly) observable have turned out to be the most useful tool in our box so far, both for analyzing and for discovering all these other phenomena – that’s why it’s still true that “we have no interest, ultimately, in grammars that generate a natural language correctly but fail to generate the correct set of structural descriptions” – Chomsky & Miller (1963:297).