For this recitation, I chose to imitate Josef Alber’s Interlocked in Processing. I chose this one because though it looks to be simple, there are some complexities within the design as well.
 (the original — Josef Albers, Interlocked, 1927, picture from Guggenheim, link to picture)
(the original — Josef Albers, Interlocked, 1927, picture from Guggenheim, link to picture)
In order to plan how I was going to code this, I started by mapping out the sketch with tentative pixel values. Inside of this map, I drew out the four larger rectangles within the piece so that I may center other elements around these. After I coded these rectangles out in Processing, I began to look at some of the repeated shapes.
Mapping out the main rectangles, after re-configuring canvas size:
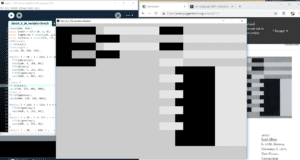
At first, I attempted to hard code all the smaller rectangles, but noticed that I could just use a for loop to increment them vertically. However, after I did this, I noticed that the width and height values I set for the other rectangle were not easily divisible, so to make things simpler, I made everything have dimensions which were divisible by 25. This helped with the positioning of things, but meant that I had to rethink all of the loops I had already created. After this was configured, finishing the rest of the sketch was rather easy.
Here’s how it looked halfway through:

One of the main challenges I faced was that I did not realize how mathematical the original painting was. Once this was configured, it made the code simpler as many things could be put in loops and incremented.
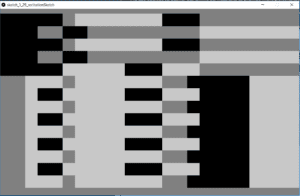
Overall, I achieved my goal of recreating this picture. Once I realized that many of the elements in the original piece are relative to other elements it was relatively easy to code with loops to increment the y position. Aside from the very graphic feel from my sketch, it looks very similar to the original.
Finished:
Thoughts:
Through this exercise, I found that math often can be found in phenomena in nature and art. As computer code cannot currently completely understand completely organic graphics, it relies on a mathematical representation. Therefore, a sort of mathematical way of thinking becomes helpful when creating art through code or designing any sort of computer graphics. Though I am not very mathematically-inclined, I enjoyed the challenge of recreating this piece of art through code.