Category: Bio-Inspired Robot Systems

Posted on

Reflection #4 – Embodied Cognitive Science

Synopsis:

This chapter of Janusz Kacprzyk and Vito Trianni’s Evolutionary Swarm Robotics deals with Embodied Cognitive Science. It goes through a history of Cognitive Science and relates it to theories such as Connectionism and Functionalism. These ideas center greatly on determining whether machines can be intelligent and defining the parameters by which a machine can be considered intelligent. 

Useful Terms and my interpretation of them:

  • Artificial Intelligence:
    • the ability of machines to mimic human reasoning
  • Cybernetics:
    • Dealing with control theory and statistical information theory
    • Forefather of Artifical Intelligence
    • Modeling agent with the environment
    • sense think act cycle (act react system)
  • Behaviourism
    • responds to a stimulus
  • Practitioners of AI
    • Value the ability to work mentally rather than responding from a stimulus
  • Unity
    • A system with boundaries that encompass a number of elementary components
    • self-organizing robotic systems
  • Connectionism
    • interconnected networks of simple units
    • symbolic spacially structured representation
  • Functionalism
    • Symbolic syntactically structured representation
  • Subsumption Architecture
    • used in behavior-based robotics
  • Situatedness
    • being in the world
  • Embodiment
    • acting in the world

Reflection:

This reading was quite technical and I found it somewhat difficult to digest. However, there were some points that stuck out to me. Firstly, I found it interesting that the claim was made that machines can never truly be intelligent because they will always be allopoeitc since they can never be living organisms (pg 19) 

This interests me because I am very intrigued by the question of whether robots need to be an artificial replica of nature to be considered successful. This seems to be the general consensus. The topic is mildly addressed in the article and made me think back to the children’s interpretation of the robotic fish. See extract below for article’s take on the question;

Not in looks, but in action, the model must resemble an animal.
Therefore, it must have these or some measure of these attributes: exploration, curiosity, free-will in the sense of unpredictability, goal-
seeking, self-regulation, avoidance of dilemmas, foresight, memory, learning, forgetting, association of ideas, form recognition, and the
elements of social accommodation. Such is life.

Grey Walter, 1953, pp. 120-121

Two other things that intrigued me were the idea of the Chinese experiment. By that logic with no intention, there can be no intelligence. By that logic artificial intelligence is a paradox in itself because while a machine can be responsive it can never achieve innate intention – Or can it? How is intention defined?

The article also brings up a valid point, we do not truly understand simple natural phenomena so how can we jump to complex cognitive thought processes. The start of robotics should look at building machines that can interact with the real world.

Posted on

Lab report 1 (Molly)

Research

1. The basic idea of a simulation game is to start with a simple configuration of counters (organisms), one to a cell, then observe how it changes as you apply Conway’s “genetic laws” for births, deaths, and survivals. Conway chose his rules carefully, after a long period of experimentation, to meet three desiderata:

1)There should be no initial pattern for which there is a simple proof that the population can grow without limit.

2)There should be initial patterns that apparently do grow without limit.

3)There should be simple initial patterns that grow and change for a considerable period of time before coming to end in three possible ways: fading away completely (from overcrowding or becoming too sparse), settling into a stable configuration that remains unchanged thereafter, or entering an oscillating phase in which they repeat an endless cycle of two or more periods.

In brief, the rules should be such as to make the behavior of the population unpredictable.

2.Variations:

It’s possible even, to create patterns which emulate logic gates (and, not, or, etc.) and counters. Building up from these, it was proved that the Game of Life is Turing Complete, which means that with a suitable initial pattern, one can do any computation that can be done on any computer. Later, Paul Rendell actually constructed a simple Turing Machine as a proof of concept. Although Rendell’s Turing Machine is fairly small, it contains all of the ideas necessary to create larger machines that could actually do meaningful calculations. One of the patterns in Jason Summers’ collection will compute prime numbers, and another will compute twin primes (two primes that only differ by adding or subtracting 2).

A very far zoom out of Paul Rendell’s Turing Machine:

NYU Web Publishing

Code examples

https://scratch.mit.edu/projects/74524028/editor/

There are 12 presets inside that can get you to experience some of the basic patterns of the game of life.

NYU Web Publishing

Tinker

Rules:

  1. Survivals. Every counter with two or three neighboring counters survives for the next generation.
  2. Deaths. Each counter with four or more neighbors dies (is removed) from overpopulation. Every counter with one neighbor or none dies from isolation.
  3. Births. Each empty cell adjacent to exactly three neighbors–no more, no fewer–is a birth cell. A counter is placed on it at the next move.

Change :

NYU Web Publishing

“3.Births. Each empty cell adjacent to exactly four neighbors–no more, no fewer–is a birth cell. A counter is placed on it at the next move.”

Example result:

  1. 5 straight lines

Under original rules:

Under changed rules:

2.Glider gun

Under original rules:

Under changed rules:

Reflection

The result contradicts with the third rule mentioned in my research that the simple initial patterns don’t grow and change for a considerable period of time before fading away completely. “Four” is a too strict requirement.

Conway’s 3 rules balance the whole system well and there may not be another set of rules which only change the number of this one that can achieve such result that disturbs the boundary between order and chaos.

Works Cite

1. Gardner, M. (1970). The fantastic combinations of John Conway’s new solitaire game “life” (pp. 120-123). Scientific American 223.

2. Conway’s Game of Life: an Overview. (2019). Retrieved from http://edshare.soton.ac.uk/948/5/intro/gameoflife.html

Posted on

Lab Report 1 by Diana Xu

Research:

I did research on how different cellular automata vary from each other. I found all of the rules for one-dimensional cellular automata. Of the 2^8=256  elementary cellular automata, there are 88 fundamentally inequivalent rules (Wolfram 2002, p. 57).

Then I read chapter 7 in Dan Shiffman’s “The Nature of Code”, which explains the algorithms of cellular automata, Wolfram classification, the game of life and variations of cellular automata. Besides the explanations of the algorithms, Dan Shiffman mentioned that there are a lot of possibilities for people to explore the variations of cellular automata. He summarized them in seven categories in below( unfortunately I only found a code example for the first category) :

Non-rectangular Grids:

Example: The shape is a hexagon cell.

Hexagons

Probabilistic:

Example: In the Game of Life, the chance to die with four or more neighbors is 80%.

Continuous:

Example: Now, the state of cells is only 0 or 1. What if it’s a floating point?

Image Processing:

Example: Pixel is a cell and color is a state

Historical:

Example: “Visualize the Game of Life by coloring each cell according to how long it’s been alive or dead”

Moving cells:

Example: “Use CA rules in a flocking system. What if each boid had a state (that perhaps informs its steering behaviors) and its neighborhood changed from frame to frame as it moved closer to or further from other boids?”

 Nesting:

Example: Each CA cell is another smaller CA system.

Based on the algorithm of CA and Game of Life, Dan Shiffman created a 2D water effect: 

Screenshot of running the code
Effect implemented with shading and refraction

Find code examples:

Hexagon Cells

Game of Life OOP

2D Water

Tinker one implementation:

Original effect: 

Tinkered effect: 

Reflect:

Cellular automata are widely used in computer science, mathematics, physics, and biology. After my research, I found the cellular automata model can also be used in the field of arts, especially generative arts and nature of code.

The 2D water example combines physics and CA algorithm. It also uses pixel manipulation. And this algorithm can also combine with image processing since the concept of state and cell is widely used in pixel manipulation.

Reference: 

“Elementary Cellular Automaton.” From Wolfram MathWorld, mathworld.wolfram.com/ElementaryCellularAutomaton.html.

Shiffman, Daniel. “THE NATURE OF CODE.” The Nature of Code, natureofcode.com/book/chapter-7-cellular-automata/.

2D water tutorial by Dan Shiffman

Posted on

Cellular Automata Lab // Konrad Krawczyk

  1. Review

Cellular automata (CA in short) are essentially programs that consist of the following components: (1) a discrete space of dimension n G Z divided in cells; (2) a finite set of possible states for each cell; (3) a certain number (the same for all cells) of neighboring cells; and (4) a transition rule that fixes the next state each cell as a function of its current state and the state of its neighbouring cells. (Gil & Alfonesca)

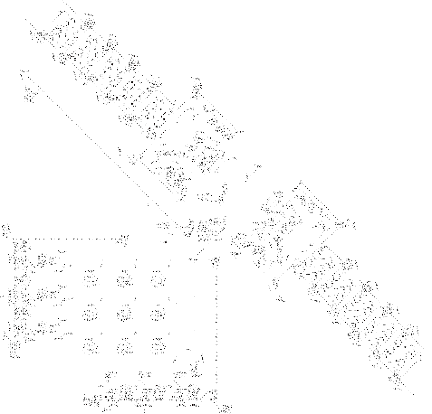
There is an elementary, one-dimensional subset of CA. In an elementary cellular automaton, the state of next generation of cells is determined by the state of that cell and its two neighbours in the current generation.

It is deemed one-dimensional since it can be easily expressed as a single, one-dimensional array. However, instances of ECA are usually expressed on two-dimensional planes, with each subsequent generation on an y-axis and order of cells on an x-axis.

A curious property of ECA is that their rule sets can often be represented in 8-bit binary sequences. 8 possible combinations of triads of binary (standing for one cell and its two neighbours) are defined in a descending order. Then for each triad, a resulting cell in the future generation is defined as either 0 or 1.

Hence, different variations are named after their the decimal equivalents of binary sequences, for example Rule 90 (standing for 01011010) or Rule 110 (01101110).

Elementary cellular automata are explored in depth in a controversial book called “A New Kind if Science” by S. Wolfram. His main thesis (and the main controversy related to the book) is that there’s a new kind of complexity-related scientific inquiries to be made, which can largely explain the complex mechanisms of chemistry, biology, and more.

He is using several examples of ECA to support his thesis. Various combinations of rules can generate simple patterns such as checkerboard (Rule XXX). A slightly more complex one is the Sierpinski Triangle (Rule 30) which stands for a series of symmetrical triangles that form a repetitive, steadily increasing pattern of triangular shapes.

Wolfram takes it a step further and focuses more on rules that generate asymmetry, complexity, or even randomness. An example of that is Rule 110. Based on a relatively simple ruleset, a pattern is generated that does not repeat itself, while generating convergences and similarities in certain parts of its growth. It is, as Wolfram would describe it, on the boundary between predictable and unpredictable.

The further part of this paper will focus specifically on implementations of elementary cellular automata, including one written by myself. Further, different approaches will be compared for efficiency and accuracy.

2. Implementations:

2.1. Devin Acker’s rules for automata

https://github.com/devinacker/celldemo/blob/gh-pages/index.htm

The program is a simple implementation written in JavaScript, and drawn in an HTML canvas element. The preview is publicly available both as a GitHub repository and a standalone website.

The simple user interface enables the user to pick a specific rule of the automaton, as well as choose a starting condition. After the user clicks “Start” the function draw_row() runs every 10 milliseconds. (This creates 100 rows per second).

This implementation creates one-dimensional data. Two arrays are running at the same time, current and next. After data is read and matched, next becomes current, and then the function is invoked again after 10 milliseconds.

2.2. p5.js reference

https://p5js.org/examples/simulate-wolfram-ca.html

A somewhat simpler implementation (albeit lacking a GUI) has been created for the purposes of p5.js reference. Here, the update rule is invoked in the draw() loop, which means a new row is drawn every time a frame is updated (30 times per second).

The program creates new generations and draws them at once. One generation at a time is created. Previous generations are not stored anywhere.

Rules are written down as a series of three-conditional statements. There is a variable ruleset that can be changed by altering the ruleset array.

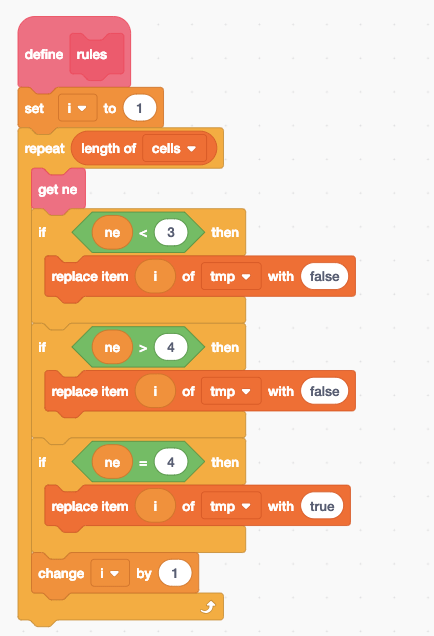
2.3. Custom implementation

https://editor.p5js.org/krawc/sketches/Fn7Yj4U78

Before exploring any other implementations, I have created my own one. It was based solely off of the general rules of cellular automata found in the Wolfram’s book and various online resources.

The main difference from the two other implementations is its two-dimensionality. Values are stored in an array of arrays, accessible anywhere in the code. This means rules can be created that use further-up rows, or farther neighbours.

The entire image is generated at once, so one cannot see the progress of it – just the end result.

Due to design of this implementation, values are being stored in an easily accessible two-dimensional array. This means I can tinker with various arrangements of triads – instead of just taking three cells next to each other, I can get cells 5 steps away rom each other, or cells from upper rows.

Here are several of the more complexity-generating variations of the original algorithm.

     

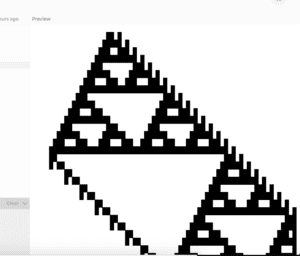
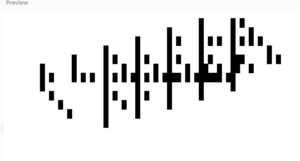
Reflection:

Somewhat accidentally, I ended up with an implementation that was more versatile than the two other ones. It was mostly because it had an easily accessible memory of previous generations.

It’s fairly easy to generate Rule 30, Rule 90 or 110, by simply providing a byte string in function setup().

Some of the variations are actually complex enough to mimic random behaviour. This is something that perhaps, with an appropriate offset, could be used as a generator for random QR codes.

Either way, elementary cellular automata constitute a curious case of phenomena that border between predictable and random. This is especially visible in case of Rule 110, which has shown to generate intricate complexities.

These phenomena, although not independent from the legacy of previous sciences (mostly mathematics), let us reflect and pose questions about the nature of science. Is not science precisely about trying to find patterns and makes sense of the “chaotic”? If we cannot directly observe events such as the origination of the universe, or of life on Earth, can cellular automata point us at the right direction at explaining the complexity?

Even in cellular automata, there has to be a condition that starts the chain of events, and that one is usually chosen arbitrarily. Nevertheless, I think generative complexities like ECA are a useful simulation tool.

References:

Gil, F. J., & Alfonseca, M. (2013). Fine Tuning Explained? Multiverses and Cellular Automata. Journal for General Philosophy of Science, 44(1), 153-172. doi:10.1007/s10838-013-9215-7

Wolfram, S. (2002). A new kind of science. Champaign: Wolfram Media.
 
Posted on

Lab Report: Cellular Automaton

Research theory

The “Game of life”, as Martin Gardner analyzed, was structured by applying simple rules that can make the population unpredictable, and also let the cells birth and die simultaneously to warrant every single generation of life becomes a “move” in the “life history” of the original cells.

Zhigang Shao and Tao Chen did some researches for the final consistent density of live cells in the EDR lattice.

The density of live cells ρ(t) as a function of time t at the lattice for ρ0 = 0.2, 0.35, and 0.5 with the system with size L=104

They first applied three initial values of the density with a size of 10 to the fourth power and noticed that some of the graphs end up with the density closes to 0.37 eventually.

https://link.springer.com/content/pdf/10.1007%2Fs10955-010-0092-8.pdf
The stable point ρ as a function of the initial density of live sites ρ0

Then they applied a number of initial density to the graphs and surprisingly found out that the initial densities between about 0.25 to 0.6 will all finally end up with a density of 0.37.

https://link.springer.com/content/pdf/10.1007%2Fs10955-010-0092-8.pdf
The stable point of density of live cells ρ as a function of system size L

Later on, they expended the range to a larger size and proved that the phenomenon appears at the scale of 10 to the fourth power is not a specific coincidence, and applied the MFA to get the density result of 0.37017.

At last, they used the MC simulation jumped to the conclusion that the final consistent density of live cells is 0.37± 0.003.

Besides, the essay that really surprised me is Carter Bays’s “Candidates for the Game of Life in Three Dimensions”. He successfully found several decent rules for the three-dimensional version of the “Game of life”, which is the discovery that I have thought of but never virtually done. The three-dimensional version truly provides a new perspective to comprehend the game and squared the fun of the game to a higher altitude.

Find code examples

automata cellular basic 1 by Tomas de Camino

https://www.openprocessing.org/sketch/130643

This implementation initials the pixels by lines and makes them change their color gradually according to the color of the pixels around them.

Cellular Automata for Diffusion by aa_debdeb

https://www.openprocessing.org/sketch/294197

This implementation changes the brightness and the size of the circle fixed on the board according to their nearby neighbors’ status.

Cellular Automata3 by Chun-Ju, Tai

This implementation shows the cells in circles and applied the algorithms to calculate the size, the color, and the position of the circles to create a beautiful graph of cellular automata.

Tinker the implementations

Changed the rectangles into ellipses
Changed the rectangles into shades from rectangles to ellipses
Applied more red to the graphs (An interesting discovery is the shining line coming from the corner)

[The code is posted below]

/*Tomas de Camino
para el taller de rogramacion de MDI veritas
Base para armar un automata celular.
*/

//Adjusted by Yile Xu

//construye el arreglo para el automata celular
int spaceSize = 100;
float rectSize;
int[][] cellSpace = new int[spaceSize][spaceSize];

void setup() {
size(600, 600);
//inicializa las celdas
for (int i =0; i < spaceSize; i++) {
for (int j =0; j < spaceSize; j++) {
cellSpace[i][j] = i*j;
}
}
rectSize = width / spaceSize;
colorMode(HSB, 100*100, 100, 100);
}

void draw() {
noStroke();
smooth();
for (int i =0; i < spaceSize; i++) {
for (int j =0; j < spaceSize; j++) {
fill( cellSpace[i][j],50, 150);
ellipse(i*rectSize, j*rectSize, rectSize, rectSize);
fill( cellSpace[spaceSize-i-1][spaceSize-j-1], 255,100);
ellipse(i*rectSize, j*rectSize, rectSize, rectSize);
//para que sea ciclico
if (cellSpace[i][j]>=10000) {
cellSpace[i][j]=0;
}
else {
cellSpace[i][j]+=10;
}
}
}
}

Reflect

The “Game of life” is really a brilliant invention conducted by Conway. And by applying a different shape, different color, and even different dimension to the game, some other implementations made by the other scientists show us the various possibilities of it.

On the path of discovery, we all need faith to go not only deeper, but also boarder. Sometimes a tiny theme looks as simple as the “Game of life” could derive to multiple expansions and applications.

Moreover, this tiny game gave us lots of thought related to our topic “bio-inspired robot system”. For instance, what does it look like if cellulars was affected by their neighbors? How might the whole part of cellulars evolve and is there an end for it, where is the end of it? These are all valuable thoughts the game virtually brings to us.

Reference

MATHEMATICAL GAMES——The fantastic combinations of John Conway’s new solitaire game “life”, by Martin Gardner, Scientific American 223 (October 1970): 120-123.

http://www.autzones.com/din6000/textes/semaine04/Gardner%20(1970)-Games.pdf

Game of Life on the Equal Degree Random Lattice Zhigang Shao · Tao Chen

Received: 11 May 2010 / Accepted: 1 November 2010 / Published online: 11 November 2010 © Springer Science + Business Media, LLC 2010.

https://link.springer.com/content/pdf/10.1007%2Fs10955-010-0092-8.pdf

complex Systems 1 (1987) 373-400, Candidates for the Game of Life in Three Dimensions’, Carter Bays, Department of Computer Science, University of So uth Carolina, Columbia, SC 29208, USA

https://pdfs.semanticscholar.org/c865/e0d19f53ba646e076d6e542e1002c92fd3ad.pdf

automata cellular basic 1by Tomas de Camino

https://www.openprocessing.org/sketch/130643

Cellular Automata for Diffusion by aa debdeb

https://www.openprocessing.org/sketch/294197

Cellular Automata3by Chun-Ju, Tai

https://www.openprocessing.org/sketch/644405