Category: Bio-Inspired Robot Systems

Research

A cellular automaton is a system of items on a grid that are either turned on or off, depending on specific rules that determine the next generation of items. These items are referred to as ‘cells’. In the simplest version of this system, a binary one-dimensional cellular automaton, each generation is represented as a horizontal line filled with squares that are either colored white (which means the cell is dead) or black (which means the cell is alive). Since the line is only a one-dimensional space, each cell will only have two neighbors, and the state of all three cells in a group (I.E. the cell in question, and its neighbor to the left and right) will be taken into account when determining the next iteration, of cells, which is seen in the next line. Dead cells are represented by a 0, and live cells are represented by a 1. Every set of 3 cells (I’ll refer to them as ‘parents’), through its combination of states, of which there are 8 possible, will determine the state of a cell below, which will always be either a 0 or a 1. A rule can be established to determine the next iteration in an “if this then that” fashion. In this case, “this” will be one of the 8 possible combination of parents, and “that” will be either 1 or 0. A single takes into account all 8 possible combinations of parents, and gives an output in the form of a combination of eight 0s and 1s. The eight different inputs in each rule are ordered as follows: 111, 110, 101, 100, 011, 010, 001, 000. There are 256 possible rules, categorized by their output, which will coincidentally be the binary form of a number between 0 and 255 (before 128, the first number represented with 8 digits in binary, a zero fills in the blanks until the number’s binary representation begins). For example, rule 30, the most famous rule, is 00011110 (30 in binary is 11110), and rule 220 is 11011100. These cellular automata often will exhibit a pattern when executed with a non-random starting point. Depending on the rule, we may see patterns like fractal-like structures or combinations of lines and triangles we could find a trend for, except for rule 30, for which I couldn’t find a pattern when I tested it, which is the reason why it is the most famous of the rules.

For this lab, given that as of the moment I find myself unable to code and program, I found a code on scratch.mit that was able to run al 256 rules on both random and non-random starting points, or seeds, the reference to which can be found under “references”. I also found on Wolfram MathWorld visual examples of some of the rules, which allowed me to explain their structure earlier in this document, as well as pictures of the 256 rules. I could not analyze in depth all the 256 pictures, but was unable to find a pattern in rules 86, 135, 149, 169 and 225. Since I was unable to modify the code I found, I chose to tinker with it by taking 3 different rules (rule 30, and two rules obtained through a random number generator, which were 114 and 163), and testing them on both a random and non-random seed. Because I saw the pictures of the 256 rules, I knew what I would find with a non-random seed; however, I wanted to see if I could find the same pattern when using a random seed.

Codes used
The code I used, which was able to display all the 256 rules, can be found here: https://scratch.mit.edu/projects/44786142/

Tinkering:
Rule 30 with a non-random seed:

Rule 30 with a random seed:

Rule 114 with a non-random seed:

Rule 114 with a random seed:

Rule 163 with a non-random seed:

Rule 163 with a random seed:

Reflection
I was able to find patterns in both rule 163 and 114 when I tried them with a random seed, and did not find one with rule 30, as I thought. With a random seed, I.E. the first line arranged randomly, we will see similar iterations for each rule, except for rule 30 and the other rules I could not find a pattern for when I looked at the 256 pictures. This shows that, just like in nature, we can find patterns in randomness. If we extrapolate this into a more complicated cellular automaton, like “Game of Life”, we will see that most patterns of cells tend to stabilize and get into a repetitive pattern relatively quickly, and we will always be able to predict the next iteration, no matter how complicated, which leads me to question the existence of true random behaviors.

References:

“Cellular Automaton.” From Wolfram MathWorld, 18 Feb. 2018, mathworld.wolfram.com/CellularAutomaton.html.

“Elementary Cellular Automaton.” From Wolfram MathWorld, 18 Feb. 2018, mathworld.wolfram.com/ElementaryCellularAutomaton.html.

Anand Tyagi

Cellular Automata Lab Report

Research:

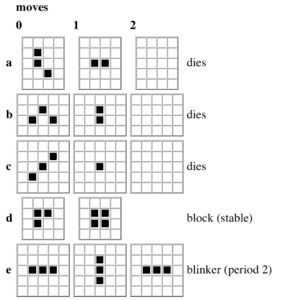
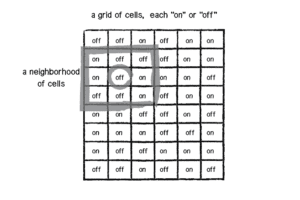
In the 1960’s, Cambridge University’s math faculty common room hosted a group of professors and students who both played and made board games. One of those games was made by a John Conway, a member of the staff, who had made a “cellular automaton on a square grid” (Bellos 262) called the Game of Life. Although it has relatively simple rules, Conway quickly noticed the multitude of different arrangements that could be made and their effects. Although the game— although it is more of a experiment rather than a game, in the traditional sense— was originally “played” by hand on a Go board (Bellos 264), it was eventually picked up by the computer programming community when Martin Gardner wrote about the Game for the Scientific American (Bellos 266) after which point it became a cultural phenomenon.

At one point, Conway offered a $50 prize for whoever could make pattern which grew continuously (Bellos 267). It was only after Bill Gosper made the “glider gun” and “eater” that “Life might have a real world application.” (Bellos 267). Throughout the following years, many individuals used Life to make patterns to make unique calculations, such as one that would “calculate the value of pi” or simulate the sieve of Eratosthenes (Bellos 268). Eventually, Conway discovered that it would be possible to build a “Life computer” by simulating logic gates through certain patterns (Bellos 269). After proving that virtually any computer program could be simulated through the creation of a “Life computer,” Conway lost interest in the problem (Bellos 270). However, plenty more continued playing with different configurations and went on to discover new patterns to eventually lead to the creation of a “Life Computer” (Bellos 272). One dedicated Lifers’ efforts, Paul Chapman, resulted in a new pattern known as the Herschel which “opened up the tantalizing possibility of self-replicating creatures in Life.” (Bellos 272).

Chapman’s work and the realization that the Game of Life could lead to insights regarding the creation of self-replicating creatures is important to answering the questions posed by John von Neumann. von Neumann questioned “how a computer might build an identical copy of itself (Bellos 273). While it was relatively easy to create a machine that can self-replicate, the main challenge came with figuring out how to send a copy of the “blueprint” or replication instructions onto the new creation. Although Chapman tried to make a self-replicating pattern, he faced the same problem of trying to replicate the blueprint. It was not until 2010, when Andrew Wade made Gemini— a self-replicating pattern which had the blueprint move between the two constructors, rather than replicate the blueprint completely (Bellos 274).  Gemini pushed “the next stage of Life exploration” (Bellos 275) allowing us to now ask if factors from our own evolution— such as Darwinian natural selection— will take place in a self-replicating system that has minor differences (Bellos 276). Thus, Conway’s simple Game of Life has turned into a template for making discoveries about the nature of our own lives.

Code examples:

Some different variations of the Game of Life include HighLife and 3D Life and closely related to Conway’s Game of Life is 1D Cellular Automata developed by Stephen Wolfram. HighLife is a version of the Game that includes the rule that if a dead cell is surrounded by 6 live cells, it comes to life. This extra addition had a replicator pattern that was able to make a copy of itself— something that has not been found in the Game of Life (excluding Gemini which does not make a self-replicating pattern, but rather, a system that is able to self replicate).

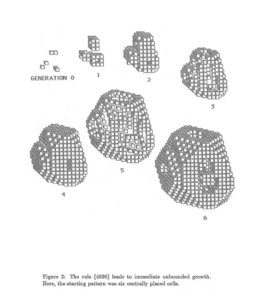
3D Life takes Conway’s creation to a higher dimension with a slightly modified set of rules. Carter Bays, the person who made this version of the Game, surprisingly found 3D gliders and oscillators in this version.

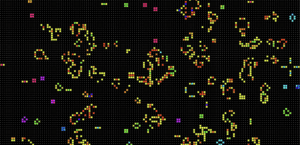
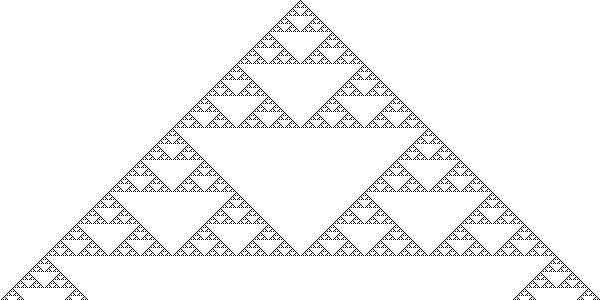
Finally, Wolfram’s 1D Cellular Automata has shown to have various outcomes based on the different set of rules that are applied to it. Certain Rule, such as a Rule 90, has shown to make patterns such as Sierpinski’s Triangle. Other rules, like Rule 30, create seemingly random patterns.

Rule 30:

Rule 90:

Reflection:

The Game of Life is simple enough for a child to understand, but regardless of its simple set up, it seems to hold the secrets to questions that have plagued us for decades. While the current version of the Game may not help us create the self-replicating robots of the future, I believe it sets the groundwork that can be used to expand von Neumann’s vision. As shown by the HighLife set of rules, if we continue to play around with the rules of the game, we may discover system that can make truly self replicating systems. Besides this more futuristic aspect, the Game of Life can also shed some light on the origins of life. Simple pieces coming together to form complex and seemingly live systems is interestingly similar to how the elemental building blocks of our universe come together to form organically complex life forms. Along with that, I wonder if the Game of Life can be taken to higher dimensions. As we have seen, Cellular Automata has been observed in 1, 2, and 3 Dimensions. But I am curious to see how 4 or higher dimensional cellular automata can be constructed or conceived, and moreover, if the basic rules of the Game of Life can be applied to higher dimensions to help solve mathematical or computational questions that take place in higher dimensions. Although Conway himself may not be confident that there is anything significant to learn from his creation, I am confident that the Game of Life has plenty more secrets for us to discover.

Citation:

Bellos, Alex, and Surreal McCoy. The Grapes of Math: How Life Reflects Numbers and Numbers Reflect Life. Simon & Schuster, 2015.

Carter Bays, The Game of Three-dimensional Life, unpublished document

“Highlife (Cellular Automaton).” Wikipedia, Wikimedia Foundation, 3 Nov. 2017, en.wikipedia.org/wiki/Highlife_(cellular_automaton).

“Kaleidoscope of 3D Life.” Crucibleteachnotes.html, Charles Pennell, 2000, www.ibiblio.org/e-notes/Life/Game.htm.

Wong, Timm. “Variations on the Game of Life.” Variations on the Game of Life, Sept. 2008, kaytdek.trevorshp.com/projects/computer/neuralNetworks/gameOfLife2.htm.

John Conway’s ‘Game of Life’ is especially intriguing in that he managed to essentially re-create the cycle of life according to his own terms. Of course, at first glance, the simulation may seem impossibly complicated, but by understanding a few simple ‘genetic laws’, the average reader will be able to get a feel for how the game unfolds. 

Taking a snippet from Martin Gardner’s article, “Mathematical Games: The Fantastic Combinations of John Conway’s New Solitaire Game ‘Life’”, we can list the basic genetic laws that govern the game of life:

“1. Survivals. Every counter with two or three neighboring counters survives for the next generation.

2. Deaths. Each counter with four or more neighbors dies (is removed) from overpopulation. Every counter with one neighbor or none dies from isolation. 

3. Births. Each empty cell adjacent to exactly three neighbors— no more, no fewer — is a birth cell.”

    – Gardner (2)

Both birth and death happen simultaneously, resulting in the myriad of changes within the patterns of cells. Cells can take on many forms, including the stabilized ‘blocks’ and alternating ‘blinkers’, as illustrated by the graphic below. 

In order to create such a simulation, Conway made use of three basic methods for constructing a working cellular automata:

• Grid: space where the cells reside (can exist on a finite number of dimensions)
• State: usually represented by “0” and “1” as “off” and “on” respectively, but a cell can have a varying number of states
• Neighborhood: a list of adjacent cells

With these basic methods, variations of Conway’s cellular automata can be created:

Cyclic Cellular Automata: https://github.com/phasenraum2010/cyclic-cellular-automaton

WireWorld: https://rosettacode.org/wiki/Wireworld

Rainbow: https://github.com/Tebs-Lab/conways-game-of-life

Though these variations are similar to Conway’s original simulation, they differ in many aspects, including dimensional changes, color changes, and addition of new rules. The Rainbow variation contains cells that are colored based on the average color values of parent cells, thereby introducing new patterns. The Cyclic Cellular Automata utilizes a different set of rules; a hierarchy of colors is established in the beginning, and whenever a cell is neighbored by another cell with a color that is next in the ‘cycle’, it does not undergo a state change. Lastly, the Wireworld variation simulates electronic circuits, and has each cell represent an electron flowing through conductors. This simulation operates on four basic rules that differ slightly from Conway’s; empty cells are always empty (black cells), electron heads (blue cells) become electron tails in the succeeding generation, electron tails (red cells) become conductors, and conductors (yellow cells) become electron heads if exactly one or two neighboring cells are electron heads. 

Tinker (pre)

Tinker (after)

Going off of the Rainbow variation for Conway’s game of life, I changed the original symmetry of the sketch, and morphed the rectangles into ellipses. Instead of the colors changing gradually like a gradient, the colors in the tinkered sketch pulsate according to the average color scheme of the parent cells in the neighborhood. 

Reference

Gardner, Martin. Mathematical Games: The Fantastic Combinations of John Conway ‘s New Solitaire Game ‘Life’. web.stanford.edu/class/sts145/Library/life.pdf.

Gardner, Martin. Mathematical Games: The Fantastic Combinations of John Conway ‘s New Solitaire Game ‘Life’. web.stanford.edu/class/sts145/Library/life.pdf.