John Conwayâs âGame of Lifeâ is especially intriguing in that he managed to essentially re-create the cycle of life according to his own terms. Of course, at first glance, the simulation may seem impossibly complicated, but by understanding a few simple âgenetic lawsâ, the average reader will be able to get a feel for how the game unfolds.
Taking a snippet from Martin Gardnerâs article, âMathematical Games: The Fantastic Combinations of John Conwayâs New Solitaire Game âLifeââ, we can list the basic genetic laws that govern the game of life:
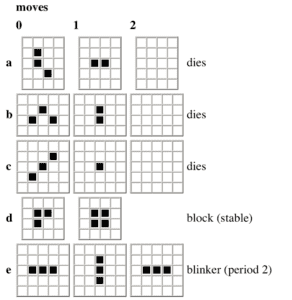
â1. Survivals. Every counter with two or three neighboring counters survives for the next generation.
2. Deaths. Each counter with four or more neighbors dies (is removed) from overpopulation. Every counter with one neighbor or none dies from isolation.
3. Births. Each empty cell adjacent to exactly three neighborsâ no more, no fewer â is a birth cell.â
– Gardner (2)
Both birth and death happen simultaneously, resulting in the myriad of changes within the patterns of cells. Cells can take on many forms, including the stabilized âblocksâ and alternating âblinkersâ, as illustrated by the graphic below.
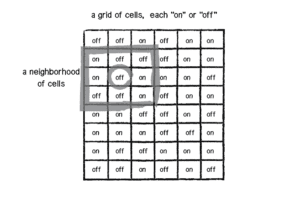
In order to create such a simulation, Conway made use of three basic methods for constructing a working cellular automata:
- Grid: space where the cells reside (can exist on a finite number of dimensions)
- State: usually represented by â0â and â1â as âoffâ and âonâ respectively, but a cell can have a varying number of states
- Neighborhood: a list of adjacent cells
With these basic methods, variations of Conwayâs cellular automata can be created:
Cyclic Cellular Automata: https://github.com/phasenraum2010/cyclic-cellular-automaton
WireWorld: https://rosettacode.org/wiki/Wireworld
Rainbow: https://github.com/Tebs-Lab/conways-game-of-life
Though these variations are similar to Conwayâs original simulation, they differ in many aspects, including dimensional changes, color changes, and addition of new rules. The Rainbow variation contains cells that are colored based on the average color values of parent cells, thereby introducing new patterns. The Cyclic Cellular Automata utilizes a different set of rules; a hierarchy of colors is established in the beginning, and whenever a cell is neighbored by another cell with a color that is next in the âcycleâ, it does not undergo a state change. Lastly, the Wireworld variation simulates electronic circuits, and has each cell represent an electron flowing through conductors. This simulation operates on four basic rules that differ slightly from Conwayâs; empty cells are always empty (black cells), electron heads (blue cells) become electron tails in the succeeding generation, electron tails (red cells) become conductors, and conductors (yellow cells) become electron heads if exactly one or two neighboring cells are electron heads.
Tinker (pre)
Tinker (after)
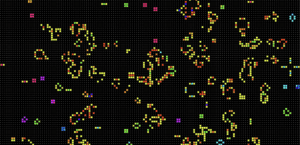
Going off of the Rainbow variation for Conway’s game of life, I changed the original symmetry of the sketch, and morphed the rectangles into ellipses. Instead of the colors changing gradually like a gradient, the colors in the tinkered sketch pulsate according to the average color scheme of the parent cells in the neighborhood.
Reference
Gardner, Martin. Mathematical Games: The Fantastic Combinations of John Conway ‘s New Solitaire Game ‘Life’. web.stanford.edu/class/sts145/Library/life.pdf.
Gardner, Martin. Mathematical Games: The Fantastic Combinations of John Conway ‘s New Solitaire Game ‘Life’. web.stanford.edu/class/sts145/Library/life.pdf.
