Author: Terrence Tu

1. Assembly

Kittenbot:

End Product:

In the assembly process,  I don’t think the sequence of assembly steps is very reasonable. The servo is the very first part to assemble. However protuberant servo and control chip of ultrasonic unit is a big problem when assembling the motors etc. on the other side. When I need to twist the screw very hard on the other side, I am so afraid I will broke the chip on the other side.

2. Coding

I decide to make an ultrasonic obstacle avoidance program. Ultrasonic unit and servo unit will be used. On start, I set the ultrasonic unit to the straight ahead. Then the kittenbot will move forward and show green light. If it meets obstacle, the light will turn red and it will pause and turn left for 90 degrees. During each pause, ultrasonic unit will swing left and right to simulate the process of detecting.

3. Effects Display

4. Reflection

Broadly, the program is successful. However, there is several minor problem. First, servo is not able to turn ultrasonic unit to straight ahead. The problem was solved when I set the servo to turn to 70 on start. I assumed it to be hardware problem. The other problem is that if the obstacle is lower than the height of ultrasonic unit, then kittenbot will not stop when it meets the obstacle. Following video shows the problem. However, it is still a hardware problem. Thus I will consider it to be minor problem.

Topic of Week Two’s lab is Robot Brain. Basically I used the MakeCode Editor to make programs for micro:bit, which is a tiny programmable computer.

A Broken Heart, a sequential output of messages (Please ignore the stupid idea!!!)

Simulated program:

Real effect:

Heart: Crush or Coalescence, program the brain (Again Please ignore the stupid idea!!!)

Simulated Program:

Real effect:

After that, Molly and I ran tests on the radio function and we used servo to simulate  behavior of tortoise.

Radio Function (a very simple test)

Once button A is pressed on one micro:bit, the other micro:bit will show number 0. It is important to set two micro:bit in the same group when programming.

Animal Behavior

We try to simulate a simple self-defense behavior of tortoise. Once a tortoise’s head is punched or hurt, it will retract its head to its shell. The program is quite simple. The logic is shown in the following diagram.

We use the acceleration sensor to simulate hitting. The program is simple and showed below.  

At first, the head(yellow paper) is head to the outside. After it get hurt(shake the micro:bit), it will turn 180 degree(head to inside). After 5 seconds, the head will go back to initial state.

Reflection:

Personally, it is not a wonderful lab experience to me. I have not taken Interaction Lab or other IMA courses before. Thus I am totally unfamiliar with all these little robotics, sensors or whatever things. It took me a while to get started. Thus, I am only able to write very simple program in the rest of the time. Yet it is a good opportunity for me to have a initial experience of  implementing models from observation of the natural world. Hope there will be another chance for me to go deeper in this field.

      As far as we learned from the class, we were still talking about cellular automaton below two dimensions. Conway’s Life of Game is a kind of two-dimensional cellular automation while Wolfram’s “The Crucial Experiment” of A New Kind of Science is doing one-dimensional cellular automaton and representing the its behavior in two-dimensional graph. From both of the cases, we can that significant complexity occurs from very simple programs.

      From my perspective, however, considering of the three-dimensional space we are living in, I am more curious about feasibility, meaning and possible applications of the cellular automation in three dimensions.

      In Stephen Wolfram’s A New Kind of Science, he actually discussed about the cellular automation in higher dimension in the chapter “Two Dimensions and Beyond“. As he said, “Indeed, despite what we might expect from traditional science, adding more dimensions does not ultimately seem to have much effect on the occurrence of behavior of any significant complexity”. It is expected to see that complexity will still happen when running the cellular automaton in three dimensions.

 

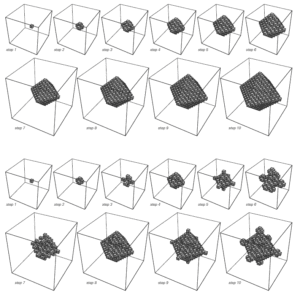
(Two examples of three-dimensional cellular automaton, Given in Stephen Wolfram’s A New Kind of Science)

     After further research, I found out some three-dimensional Game of Life. First we need to introduce a new naming method of  Game of Life.

      As we known, Conway’s Game of Life only has two  rules, one defines when to survive or die. The other one defines when to come alive. According to that, we can use a 4-tuple to define different Game of Life of different rules. Life ABCD means that (1) an alive cell survives when it touches at least A, at most B cell, it survive, otherwise it dies.(2) a dead cell comes to alive when it touches down to C, up to D cell. In this case, Conway’s Game of Life can be define as Life 2333.

      Carter Bays, in his paper “Candidates for the Game of Life in Three Dimensions”, defined that the naming method can only be used when following are True:

1.A glider must exist and must occur “naturally” if we apply repeatedly to primordial soup configurations.
2.All primordial soup configurations, when subjected to, must exhibit bounded growth.

      Carter Bays suggested that Life 4555 and Life 5766 are two best “worthy of the name” three-dimensional Game of Life. Thus, I turned to searched for some codes to test these two type of Life.

       3DGameofLife on GitHub is a JavaScript program created by Raphael Beaulieu and Elliot Coy. It can test three-dimensional Game of Life in a bounded space of 20×20×20. The complete code can be seen when we check the source code of the page, thus I am not going to paste it here. 

      First, going to test Life 4555. When I began the game with 7 cells of a 3D cross shape, The game showed a pattern of blinker. It stably iterates between three shape. 

      Then, going to run Life 4555 again. This time, I began the game with 12 cells with the following shape.

      This time, even with the same rules, cells shows a totally different pattern. The number of cells explodes in a very short of time.

       Still, running Life 4555, with 5 cells of 2D cross shape. It turned out to be a third pattern. The cross repeatedly produced itself on the both way of the same line.

      Finally, testing the rule 5677. It showed a pattern of glider. The glider moved diagonally in one plane. However, it is worth to mention that the plane is parallel with one axis and  perpendicular to the other two axis, which means that the moving of the glider is kind of restricted.

Interestingly we can see that even under same rules, the outcomes will be significantly different because of the different input parameters, even when the differences between the input parameters are quite little. From my view, it is pretty similar to the beginning of life. Even there are planets other than Earth offer exactly same condition on Earth,  Our planets may be the only one holds the promise of life. 

Also, I find out that all the patterns under three-dimensional Game of Life I achieve above can actually acquired in the two-dimensional Game of Life. To some extend, it proves Bays’ saying “adding more dimensions does not ultimately seem to have much effect on the occurrence of behavior of any significant complexity”. However, since two-dimensional space is not visible, is that possible for two-dimensional creatures that we cannot  see existed as dimension seems not to be an important factors of complexity. That will be a left question for me.

Cite:

Candidates for the Game of Life in Three Dimensions’, Complex Systems, Carter Bays, Columbia, SC 29208, USA,

https://pdfs.semanticscholar.org/c865/e0d19f53ba646e076d6e542e1002c92fd3ad.pdf

Wolfram, Stephen. “Two Dimensions and Beyond”, A New Kind of Science, 1959, Wolfram Media

https://www.wolframscience.com/nks/chap-5–two-dimensions-and-beyond/

3DGameofLife, Raphael Beaulieu, Elliot Coy

http://rbeaulieu.github.io/3DGameOfLife/3DGameOfLife.html?