By: Gabrielle Branche
Getting Ready:
My partner Kevin and I tested the microbit after downloading the code and were pleasantly surprised at how responsive it was. We used a multimeter to measure the voltage output to be 3.2V ±0.05V.
Programming the brain and using its sensors:
These sections are merged because we unintentionally programmed the brain with the simulation such that it worked on the hardware as well both inputting data and outputting accordingly. Further programming was done when trying to debug our platypus code.
We decided to program our code to turn on certain LEDs on pressing button A. Turn off these same lights when pressing button B. Additionally, we programmed it to play music when it shook. We then tinkered with the code allowing shake to manipulate the tempo of the music. At first this was difficult because we did not set up the wiring for the headphones right but we finally got it to work.
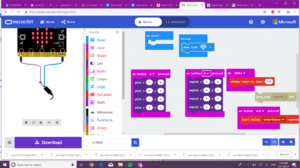
Limitations:
Since we mainly just fiddled with the different box, we realized after that we were giving ourselves unnecessary work by using less convenient code such as the plotting function.
Additionally, due to the microbit’s small grid, it is difficult to have full words shown and the user has to wait till the entire message flashes across the screen to see it.
Finally, the blocks given are quite small in variation and thus makes it hard for a beginner coder to explore all the possible uses for the bot. However, the program does provide a space to code using JavaScript which can allow for the microbot to be more useful
However even though this is a bit limiting, the microbot has the potential to be very handy as other components can be attached to it such as the headphones we used to play music.
Basic Animal Behavior System
We decided to explore the behavior of a platypus. While the exercise did not call for us to look an any particular animal we thought that by narrowing down to a specific animal we could truly explore how it operates holistically. The platypus is an animal native to Australia. It is nocturnal and is known for its acute sight and sense of hearing. As such we decided to design a program that could respond to these senses.
By using a photocell, we could execute the responses only within a specific light intensity threshold. Since the platypus is nocturnal we decided that above a certain threshold it would cease all activity.
If below the threshold the platypus could respond to sound using a sound sensor thus simulating acute hearing. If sudden loud sounds are made, the eyes of the platypus would glow and it would shake.
Finally using a proximity sensor, the platypus could be programmed to move away from obstacles within a specific distance. This thus mimics its sight which allows it to maintain a safe distance from predators.
All these actions stem from one of the basic necessities of all living things – irritability: responding to internal and external stimulus. All animals respond to stimuli differently but all girls respond to stimuli none the less.
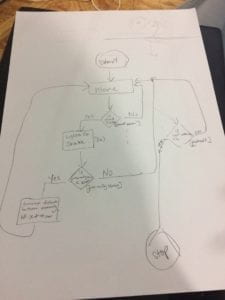
Using the microbot as the brain of the platypus, the aforementioned components can be set up to allow for execution of its animal behavior.
Connect it
Finally, we created a simplified version of the code for the microbot that maintained the core of stimulus response. Using the built-in light intensity sensor, we could provide a threshold for light. Then if button B was pressed, the platypus would make a smiley face and sing responding to ‘sound’. When it was shaken it would blink an arrow representing running away from a predator.
At first before using the light-intensity sensor the code worked well. However, there was great trouble when working with the light. The values for light intensity changes sporadically and it seemed to not response to any conditional statements that hinged on a specific light intensity. We tried to simplify the code such that above an intensity of 20, the bot would frown and below that intensity it would display a heart.
let light = 0 basic.showNumber(input.lightLevel()) light = input.lightLevel() if (light < 20) { basic.showIcon(IconNames.Heart) } if (light > 20) { basic.showNumber(IconNames.Sad) }
However, no matter how we changed the light intensity using flash lights the LEDs would not change from whatever it chose first. We hope that by using more accurate photocell and move debugging such as that done below, this experiment may work.
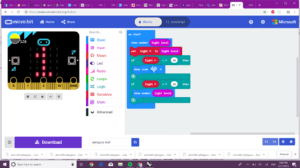
basic.showNumber(input.lightLevel()) let light = input.lightLevel() if (light < 20) { basic.showIcon(IconNames.Heart) } if (light > 20) { basic.showNumber(input.lightLevel()) }
Reflection:
This was a very useful lab because it made me realize that while the task of building a robot seemed mountainous and challenging, it is in fact a simple matter of breaking down the tasks into individual responses to stimuli. As living beings, we act through reacting, by taking into consideration how one would behave within certain conditions it becomes just a matter of having the correct syntax for creating the response. While this is not meant to invalidate the immense complexities that are found in almost all multicellular organisms, it does make starting the process of building robots significantly less daunting.