Research theory
The “Game of life”, as Martin Gardner analyzed, was structured by applying simple rules that can make the population unpredictable, and also let the cells birth and die simultaneously to warrant every single generation of life becomes a “move” in the “life history” of the original cells.
Zhigang Shao and Tao Chen did some researches for the final consistent density of live cells in the EDR lattice.
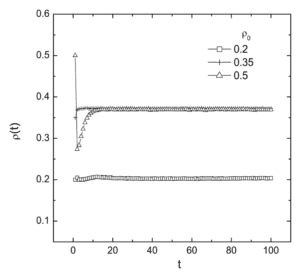
They first applied three initial values of the density with a size of 10 to the fourth power and noticed that some of the graphs end up with the density closes to 0.37 eventually.
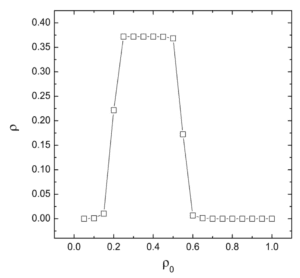
Then they applied a number of initial density to the graphs and surprisingly found out that the initial densities between about 0.25 to 0.6 will all finally end up with a density of 0.37.
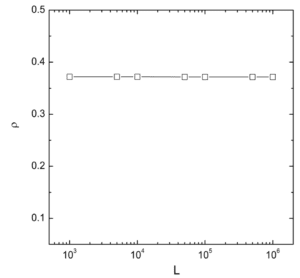
Later on, they expended the range to a larger size and proved that the phenomenon appears at the scale of 10 to the fourth power is not a specific coincidence, and applied the MFA to get the density result of 0.37017.
At last, they used the MC simulation jumped to the conclusion that the final consistent density of live cells is 0.37± 0.003.
Besides, the essay that really surprised me is Carter Bays’s “Candidates for the Game of Life in Three Dimensions”. He successfully found several decent rules for the three-dimensional version of the “Game of life”, which is the discovery that I have thought of but never virtually done. The three-dimensional version truly provides a new perspective to comprehend the game and squared the fun of the game to a higher altitude.
Find code examples
automata cellular basic 1 by Tomas de Camino

This implementation initials the pixels by lines and makes them change their color gradually according to the color of the pixels around them.
Cellular Automata for Diffusion by aa_debdeb

This implementation changes the brightness and the size of the circle fixed on the board according to their nearby neighbors’ status.
Cellular Automata3 by Chun-Ju, Tai

This implementation shows the cells in circles and applied the algorithms to calculate the size, the color, and the position of the circles to create a beautiful graph of cellular automata.
Tinker the implementations
[The code is posted below]
/*Tomas de Camino
para el taller de rogramacion de MDI veritas
Base para armar un automata celular.
*/
//Adjusted by Yile Xu
//construye el arreglo para el automata celular
int spaceSize = 100;
float rectSize;
int[][] cellSpace = new int[spaceSize][spaceSize];
void setup() {
size(600, 600);
//inicializa las celdas
for (int i =0; i < spaceSize; i++) {
for (int j =0; j < spaceSize; j++) {
cellSpace[i][j] = i*j;
}
}
rectSize = width / spaceSize;
colorMode(HSB, 100*100, 100, 100);
}
void draw() {
noStroke();
smooth();
for (int i =0; i < spaceSize; i++) {
for (int j =0; j < spaceSize; j++) {
fill( cellSpace[i][j],50, 150);
ellipse(i*rectSize, j*rectSize, rectSize, rectSize);
fill( cellSpace[spaceSize-i-1][spaceSize-j-1], 255,100);
ellipse(i*rectSize, j*rectSize, rectSize, rectSize);
//para que sea ciclico
if (cellSpace[i][j]>=10000) {
cellSpace[i][j]=0;
}
else {
cellSpace[i][j]+=10;
}
}
}
}
Reflect
The “Game of life” is really a brilliant invention conducted by Conway. And by applying a different shape, different color, and even different dimension to the game, some other implementations made by the other scientists show us the various possibilities of it.
On the path of discovery, we all need faith to go not only deeper, but also boarder. Sometimes a tiny theme looks as simple as the “Game of life” could derive to multiple expansions and applications.
Moreover, this tiny game gave us lots of thought related to our topic “bio-inspired robot system”. For instance, what does it look like if cellulars was affected by their neighbors? How might the whole part of cellulars evolve and is there an end for it, where is the end of it? These are all valuable thoughts the game virtually brings to us.
Reference
MATHEMATICAL GAMES——The fantastic combinations of John Conway’s new solitaire game “life”, by Martin Gardner, Scientific American 223 (October 1970): 120-123.
http://www.autzones.com/din6000/textes/semaine04/Gardner%20(1970)-Games.pdf
Game of Life on the Equal Degree Random Lattice Zhigang Shao · Tao Chen
Received: 11 May 2010 / Accepted: 1 November 2010 / Published online: 11 November 2010 © Springer Science + Business Media, LLC 2010.
https://link.springer.com/content/pdf/10.1007%2Fs10955-010-0092-8.pdf
complex Systems 1 (1987) 373-400, Candidates for the Game of Life in Three Dimensions’, Carter Bays, Department of Computer Science, University of So uth Carolina, Columbia, SC 29208, USA
https://pdfs.semanticscholar.org/c865/e0d19f53ba646e076d6e542e1002c92fd3ad.pdf
automata cellular basic 1by Tomas de Camino
https://www.openprocessing.org/sketch/130643
Cellular Automata for Diffusion by aa debdeb
https://www.openprocessing.org/sketch/294197
Cellular Automata3by Chun-Ju, Tai
It’s a great idea to use color to represent cells, which give them more attributes but not only alive and dead. It’s also a brilliant idea to change the shape of cells beside squares. Although it decreases the similarities between real life pattern and the algorithm, which is discrete. It is a great success to generate great pictures and offers a great possibility to study continuous objects.