Anand Tyagi, Lab 1: Cellular Automata

Anand Tyagi

Cellular Automata Lab Report

Research:

In the 1960’s, Cambridge University’s math faculty common room hosted a group of professors and students who both played and made board games. One of those games was made by a John Conway, a member of the staff, who had made a “cellular automaton on a square grid” (Bellos 262) called the Game of Life. Although it has relatively simple rules, Conway quickly noticed the multitude of different arrangements that could be made and their effects. Although the game— although it is more of a experiment rather than a game, in the traditional sense— was originally “played” by hand on a Go board (Bellos 264), it was eventually picked up by the computer programming community when Martin Gardner wrote about the Game for the Scientific American (Bellos 266) after which point it became a cultural phenomenon.

At one point, Conway offered a $50 prize for whoever could make pattern which grew continuously (Bellos 267). It was only after Bill Gosper made the “glider gun” and “eater” that “Life might have a real world application.” (Bellos 267). Throughout the following years, many individuals used Life to make patterns to make unique calculations, such as one that would “calculate the value of pi” or simulate the sieve of Eratosthenes (Bellos 268). Eventually, Conway discovered that it would be possible to build a “Life computer” by simulating logic gates through certain patterns (Bellos 269). After proving that virtually any computer program could be simulated through the creation of a “Life computer,” Conway lost interest in the problem (Bellos 270). However, plenty more continued playing with different configurations and went on to discover new patterns to eventually lead to the creation of a “Life Computer” (Bellos 272). One dedicated Lifers’ efforts, Paul Chapman, resulted in a new pattern known as the Herschel which “opened up the tantalizing possibility of self-replicating creatures in Life.” (Bellos 272).

Chapman’s work and the realization that the Game of Life could lead to insights regarding the creation of self-replicating creatures is important to answering the questions posed by John von Neumann. von Neumann questioned “how a computer might build an identical copy of itself (Bellos 273). While it was relatively easy to create a machine that can self-replicate, the main challenge came with figuring out how to send a copy of the “blueprint” or replication instructions onto the new creation. Although Chapman tried to make a self-replicating pattern, he faced the same problem of trying to replicate the blueprint. It was not until 2010, when Andrew Wade made Gemini— a self-replicating pattern which had the blueprint move between the two constructors, rather than replicate the blueprint completely (Bellos 274).  Gemini pushed “the next stage of Life exploration” (Bellos 275) allowing us to now ask if factors from our own evolution— such as Darwinian natural selection— will take place in a self-replicating system that has minor differences (Bellos 276). Thus, Conway’s simple Game of Life has turned into a template for making discoveries about the nature of our own lives.

Code examples:

Some different variations of the Game of Life include HighLife and 3D Life and closely related to Conway’s Game of Life is 1D Cellular Automata developed by Stephen Wolfram. HighLife is a version of the Game that includes the rule that if a dead cell is surrounded by 6 live cells, it comes to life. This extra addition had a replicator pattern that was able to make a copy of itself— something that has not been found in the Game of Life (excluding Gemini which does not make a self-replicating pattern, but rather, a system that is able to self replicate).

3D Life takes Conway’s creation to a higher dimension with a slightly modified set of rules. Carter Bays, the person who made this version of the Game, surprisingly found 3D gliders and oscillators in this version.

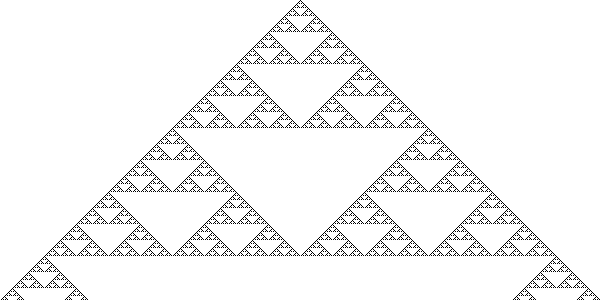
Finally, Wolfram’s 1D Cellular Automata has shown to have various outcomes based on the different set of rules that are applied to it. Certain Rule, such as a Rule 90, has shown to make patterns such as Sierpinski’s Triangle. Other rules, like Rule 30, create seemingly random patterns.

Rule 30:

Rule 90:

Reflection:

The Game of Life is simple enough for a child to understand, but regardless of its simple set up, it seems to hold the secrets to questions that have plagued us for decades. While the current version of the Game may not help us create the self-replicating robots of the future, I believe it sets the groundwork that can be used to expand von Neumann’s vision. As shown by the HighLife set of rules, if we continue to play around with the rules of the game, we may discover system that can make truly self replicating systems. Besides this more futuristic aspect, the Game of Life can also shed some light on the origins of life. Simple pieces coming together to form complex and seemingly live systems is interestingly similar to how the elemental building blocks of our universe come together to form organically complex life forms. Along with that, I wonder if the Game of Life can be taken to higher dimensions. As we have seen, Cellular Automata has been observed in 1, 2, and 3 Dimensions. But I am curious to see how 4 or higher dimensional cellular automata can be constructed or conceived, and moreover, if the basic rules of the Game of Life can be applied to higher dimensions to help solve mathematical or computational questions that take place in higher dimensions. Although Conway himself may not be confident that there is anything significant to learn from his creation, I am confident that the Game of Life has plenty more secrets for us to discover.

Citation:

Bellos, Alex, and Surreal McCoy. The Grapes of Math: How Life Reflects Numbers and Numbers Reflect Life. Simon & Schuster, 2015.

Carter Bays, The Game of Three-dimensional Life, unpublished document

“Highlife (Cellular Automaton).” Wikipedia, Wikimedia Foundation, 3 Nov. 2017, en.wikipedia.org/wiki/Highlife_(cellular_automaton).

“Kaleidoscope of 3D Life.” Crucibleteachnotes.html, Charles Pennell, 2000, www.ibiblio.org/e-notes/Life/Game.htm.

Wong, Timm. “Variations on the Game of Life.” Variations on the Game of Life, Sept. 2008, kaytdek.trevorshp.com/projects/computer/neuralNetworks/gameOfLife2.htm.