Bio-Inspired Robot Systems | Cellular Automaton by Kennedy Cambra-Cho
Research
It from Bit: Is the universe a cellular automation? by Paul Halpern Forbes Magazine
Analyzing the Influence of Mobile Phone Use of Drivers on Traffic Flow Based on an Improved Cellular Automaton Model by Yao Xiao and Jing Shi
The simple and unassuming nature of John Conway’s The Game of Life introduces the concept of cellular automaton in accessible, applicable way. Other researchers in various fields utilized Conway’s simulation to model physical phenomena and gain useful insight. In Forbes magazine’s article, “It from Bit: Is the universe a cellular automation?”, Paul Halpern asks, “Could the universe itself, at its deepest level, operate on the basis of similarly discrete digital rules?”. His question highlights the possibility of wide application for Conway’s simulation. While Halpern does note that the simplicity of the game of life can not directly translate to the simulation of reality, it can act as a bridge of thought connecting the physical world to the field of computation. He sites Ed Fredkin’s theory that “digital information could represent reality on the particle level” and would “interact as a universal cellular automaton”; however, Richard Feynman’s criticism of his theory exposes its incompatibility with the theory of quantum processes (Halpern). In order to mimic a quantum system we must be able to occupy an in-between sate that the binary system is unable to do. So, while traditional computers can not execute quantum system simulations there is a possibility that developing quantum computers may be able to in the near future.
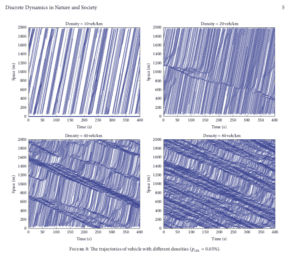
Despite the inadequacies found in simulating nature on a particle level, cellular automaton has aided in the research of other physical phenomena. Yao Xiao and Jing Shi use cellular automaton to explore the effects cell use and distracted driving has on traffic flow in their article, “Analyzing the Influence of Mobile Phone Use of Drivers on Traffic Flow based on an Improved Cellular Automaton Model”. Their resulting pattern gives us insight into the delay time caused by the select “distracted” drivers within the traffic flow. The improved model mimics the layout of a “one-way two-lane highway” measuring at 2km (closed circle). The biggest change to the model is the varying states each cell can occupy. Despite still modeling a simple on or off state, the model can categorize the cell as a distinct value of “on”. For example, each cell can be between -1 and 7; -1 meaning unoccupied and 0 -7 meaning that the car occupies the cell at a specific velocity between 0 – 7. This allows the model to calculate the resulting slow down in traffic flow. This change in the model offers more flexibility to what we can explore and infer from the produced output.
Variations of the Game of Life
(Code listed at the end)
- Python
Generation 5
- Processing
- Scratch MIT
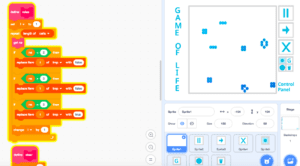
Tinker & Analyze
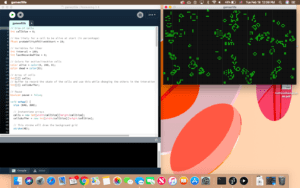
Using the Processing script I changed the Conway’s original rules to create a different pattern. I found that with my changes the sequence does not grow and contract as Conway’s did. Instead it would go through 1 or 2 sequences until it would ultimately stop at a on and off point. This “on and off point” I refer to is the event where each cell toggles between 0 and 1 repeatedly thus, creating a simple alternating pattern.
Original Rules:

Edited Rules:
https://drive.google.com/file/d/18audqIjxeddCoKfyNTD4slxuB51xJ-8c/view?usp=sharing
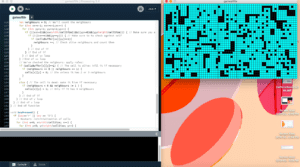
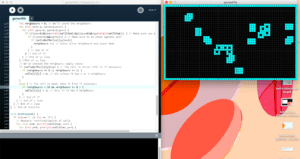
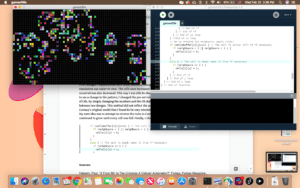
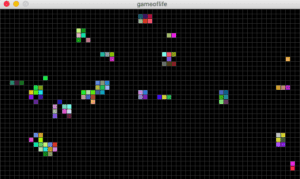
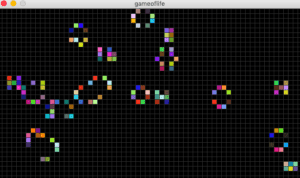



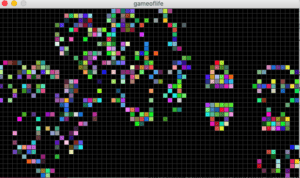
Reflection:
The concept of cellular automaton is simple to understand however, it’s active application presents some problems. Paul Halpern’s article approaches its applicability in a theoretical, removed way. In contrast, Xiao and Shi’s research presents a successful instant of active application where cellular automaton produces some useful insight into a particular phenomenon. The deceptively simple nature of John Conway’s Game of Life led me to falsely believe that the manipulation of the model would be equally simple. Xiao and Shi’s detailed documentation of their “improved” model helped me to better understand the in-depth thought that must go into model manipulation. While not completely successful, I did
First changes I implemented were small aesthetic changes and dimensional changes so that the simulation was easier to view. The cells were increased in size and the speed each generation occurred was also decreased. This way I was able to observe the incremental changes easier. In order to see a change in the pattern, I changed the pre-set rules given in Processing’s example of The Game of Life. By simply changing the numbers and the OR statements to AND the pattern would only toggle between two designs. This method did not reflect the unpredictability and “random” nature of Conway’s original model that I found to be very interesting.
My next idea was to attempt to reverse the rules in Conway’s model. This created a model that continued to grow until every cell was full. Finally, I changed the rules to:

This resulted in an exploding pattern that had a similar “random” quality.
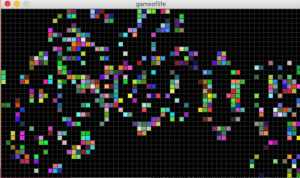
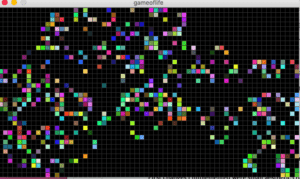
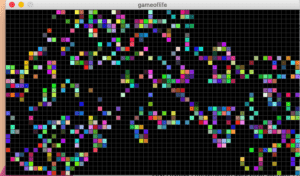
Sources:
Halpern, Paul. “It From Bit: Is The Universe A Cellular Automaton?” Forbes, Forbes Magazine,
26 Sept. 2017, www.forbes.com/sites/startswithabang/2017/09/26/it-from-bit-is-the-universe-a-cellular-automaton/#2da8379846b7
Xiao, Yao, and Jing Shi. “Analyzing the Influence of Mobile Phone Use of Drivers on Traffic Flow
Based on an Improved Cellular Automaton Model.” Discrete Dynamics in Nature and
Society, vol. 2015, 2015, pp. 1–9., doi:10.1155/2015/573090.
https://processing.org/examples/gameoflife.html
https://github.com/ctjacobs/game-of-life/blob/master/game-of-life.py
https://scratch.mit.edu/projects/280841340/editor/
https://scratch.mit.edu/projects/74524028/fullscreen/
Code
Python:
#!/usr/bin/env python
# An implementation of Conway’s Game of Life in Python.
# Copyright (C) 2013 Christian Jacobs.
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 3 of the License, or
# (at your option) any later version.
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
# GNU General Public License for more details.
# You should have received a copy of the GNU General Public License
# along with this program. If not, see <http://www.gnu.org/licenses/>.
import numpy
import pylab
import random
class GameOfLife:
def __init__(self, N=100, T=200):
“”” Set up Conway’s Game of Life. “””
# Here we create two grids to hold the old and new configurations.
# This assumes an N*N grid of points.
# Each point is either alive or dead, represented by integer values of 1 and 0, respectively.
self.N = N
self.old_grid = numpy.zeros(N*N, dtype=’i’).reshape(N,N)
self.new_grid = numpy.zeros(N*N, dtype=’i’).reshape(N,N)
self.T = T # The maximum number of generations
# Set up a random initial configuration for the grid.
for i in range(0, self.N):
for j in range(0, self.N):
if(random.randint(0, 100) < 15):
self.old_grid[i][j] = 1
else:
self.old_grid[i][j] = 0
def live_neighbours(self, i, j):
“”” Count the number of live neighbours around point (i, j). “””
s = 0 # The total number of live neighbours.
# Loop over all the neighbours.
for x in [i-1, i, i+1]:
for y in [j-1, j, j+1]:
if(x == i and y == j):
continue # Skip the current point itself – we only want to count the neighbours!
if(x != self.N and y != self.N):
s += self.old_grid[x][y]
# The remaining branches handle the case where the neighbour is off the end of the grid.
# In this case, we loop back round such that the grid becomes a “toroidal array”.
elif(x == self.N and y != self.N):
s += self.old_grid[0][y]
elif(x != self.N and y == self.N):
s += self.old_grid[x][0]
else:
s += self.old_grid[0][0]
return s
def play(self):
“”” Play Conway’s Game of Life. “””
# Write the initial configuration to file.
pylab.pcolormesh(self.old_grid)
pylab.colorbar()
pylab.savefig(“generation0.png”)
t = 1 # Current time level
write_frequency = 5 # How frequently we want to output a grid configuration.
while t <= self.T: # Evolve!
print (“At time level %d” % t)
# Loop over each cell of the grid and apply Conway’s rules.
for i in range(self.N):
for j in range(self.N):
live = self.live_neighbours(i, j)
if(self.old_grid[i][j] == 1 and live < 2):
self.new_grid[i][j] = 0 # Dead from starvation.
elif(self.old_grid[i][j] == 1 and (live == 2 or live == 3)):
self.new_grid[i][j] = 1 # Continue living.
elif(self.old_grid[i][j] == 1 and live > 3):
self.new_grid[i][j] = 0 # Dead from overcrowding.
elif(self.old_grid[i][j] == 0 and live == 3):
self.new_grid[i][j] = 1 # Alive from reproduction.
# Output the new configuration.
if(t % write_frequency == 0):
pylab.pcolormesh(self.new_grid)
pylab.savefig(“generation%d.png” % t)
# The new configuration becomes the old configuration for the next generation.
self.old_grid = self.new_grid.copy()
# Move on to the next time level
t += 1
if(__name__ == “__main__”):
game = GameOfLife(N = 100, T = 200)
game.play()
Processing:
// Size of cells
int cellSize = 5;
// How likely for a cell to be alive at start (in percentage)
float probabilityOfAliveAtStart = 15;
// Variables for timer
int interval = 100;
int lastRecordedTime = 0;
// Colors for active/inactive cells
color alive = color(0, 200, 0);
color dead = color(0);
// Array of cells
int[][] cells;
// Buffer to record the state of the cells and use this while changing the others in the interations
int[][] cellsBuffer;
// Pause
boolean pause = false;
void setup() {
size (640, 360);
// Instantiate arrays
cells = new int[width/cellSize][height/cellSize];
cellsBuffer = new int[width/cellSize][height/cellSize];
// This stroke will draw the background grid
stroke(48);
noSmooth();
// Initialization of cells
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
float state = random (100);
if (state > probabilityOfAliveAtStart) {
state = 0;
}
else {
state = 1;
}
cells[x][y] = int(state); // Save state of each cell
}
}
background(0); // Fill in black in case cells don’t cover all the windows
}
void draw() {
//Draw grid
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
if (cells[x][y]==1) {
fill(alive); // If alive
}
else {
fill(dead); // If dead
}
rect (x*cellSize, y*cellSize, cellSize, cellSize);
}
}
// Iterate if timer ticks
if (millis()-lastRecordedTime>interval) {
if (!pause) {
iteration();
lastRecordedTime = millis();
}
}
// Create new cells manually on pause
if (pause && mousePressed) {
// Map and avoid out of bound errors
int xCellOver = int(map(mouseX, 0, width, 0, width/cellSize));
xCellOver = constrain(xCellOver, 0, width/cellSize-1);
int yCellOver = int(map(mouseY, 0, height, 0, height/cellSize));
yCellOver = constrain(yCellOver, 0, height/cellSize-1);
// Check against cells in buffer
if (cellsBuffer[xCellOver][yCellOver]==1) { // Cell is alive
cells[xCellOver][yCellOver]=0; // Kill
fill(dead); // Fill with kill color
}
else { // Cell is dead
cells[xCellOver][yCellOver]=1; // Make alive
fill(alive); // Fill alive color
}
}
else if (pause && !mousePressed) { // And then save to buffer once mouse goes up
// Save cells to buffer (so we opeate with one array keeping the other intact)
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
cellsBuffer[x][y] = cells[x][y];
}
}
}
}
void iteration() { // When the clock ticks
// Save cells to buffer (so we opeate with one array keeping the other intact)
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
cellsBuffer[x][y] = cells[x][y];
}
}
// Visit each cell:
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
// And visit all the neighbours of each cell
int neighbours = 0; // We’ll count the neighbours
for (int xx=x-1; xx<=x+1;xx++) {
for (int yy=y-1; yy<=y+1;yy++) {
if (((xx>=0)&&(xx<width/cellSize))&&((yy>=0)&&(yy<height/cellSize))) { // Make sure you are not out of bounds
if (!((xx==x)&&(yy==y))) { // Make sure to to check against self
if (cellsBuffer[xx][yy]==1){
neighbours ++; // Check alive neighbours and count them
}
} // End of if
} // End of if
} // End of yy loop
} //End of xx loop
// We’ve checked the neigbours: apply rules!
if (cellsBuffer[x][y]==1) { // The cell is alive: kill it if necessary
if (neighbours < 2 || neighbours > 3) {
cells[x][y] = 0; // Die unless it has 2 or 3 neighbours
}
}
else { // The cell is dead: make it live if necessary
if (neighbours == 3 ) {
cells[x][y] = 1; // Only if it has 3 neighbours
}
} // End of if
} // End of y loop
} // End of x loop
} // End of function
void keyPressed() {
if (key==’r’ || key == ‘R’) {
// Restart: reinitialization of cells
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
float state = random (100);
if (state > probabilityOfAliveAtStart) {
state = 0;
}
else {
state = 1;
}
cells[x][y] = int(state); // Save state of each cell
}
}
}
if (key==’ ‘) { // On/off of pause
pause = !pause;
}
if (key==’c’ || key == ‘C’) { // Clear all
for (int x=0; x<width/cellSize; x++) {
for (int y=0; y<height/cellSize; y++) {
cells[x][y] = 0; // Save all to zero
}
}
}
}