Research

1. The basic idea of a simulation game is to start with a simple configuration of counters (organisms), one to a cell, then observe how it changes as you apply Conway’s “genetic laws” for births, deaths, and survivals. Conway chose his rules carefully, after a long period of experimentation, to meet three desiderata:

1)There should be no initial pattern for which there is a simple proof that the population can grow without limit.

2)There should be initial patterns that apparently do grow without limit.

3)There should be simple initial patterns that grow and change for a considerable period of time before coming to end in three possible ways: fading away completely (from overcrowding or becoming too sparse), settling into a stable configuration that remains unchanged thereafter, or entering an oscillating phase in which they repeat an endless cycle of two or more periods.

In brief, the rules should be such as to make the behavior of the population unpredictable.

2.Variations:

It’s possible even, to create patterns which emulate logic gates (and, not, or, etc.) and counters. Building up from these, it was proved that the Game of Life is Turing Complete, which means that with a suitable initial pattern, one can do any computation that can be done on any computer. Later, Paul Rendell actually constructed a simple Turing Machine as a proof of concept. Although Rendell’s Turing Machine is fairly small, it contains all of the ideas necessary to create larger machines that could actually do meaningful calculations. One of the patterns in Jason Summers’ collection will compute prime numbers, and another will compute twin primes (two primes that only differ by adding or subtracting 2).

A very far zoom out of Paul Rendell’s Turing Machine:

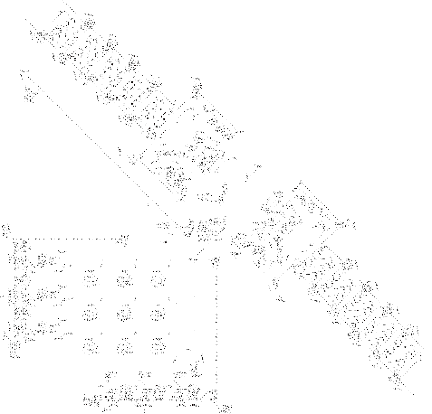
Code examples

https://scratch.mit.edu/projects/74524028/editor/

There are 12 presets inside that can get you to experience some of the basic patterns of the game of life.

Tinker

Rules:

1. Survivals. Every counter with two or three neighboring counters survives for the next generation.
2. Deaths. Each counter with four or more neighbors dies (is removed) from overpopulation. Every counter with one neighbor or none dies from isolation.
3. Births. Each empty cell adjacent to exactly three neighbors–no more, no fewer–is a birth cell. A counter is placed on it at the next move.

Change :

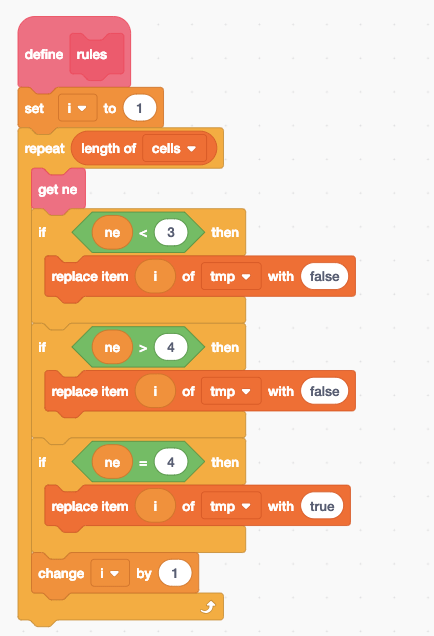
“3.Births. Each empty cell adjacent to exactly four neighbors–no more, no fewer–is a birth cell. A counter is placed on it at the next move.”

Example result:

1. 5 straight lines

Under original rules:

Under changed rules:

2.Glider gun

Under original rules:

Under changed rules:

Reflection

The result contradicts with the third rule mentioned in my research that the simple initial patterns don’t grow and change for a considerable period of time before fading away completely. “Four” is a too strict requirement.

Conway’s 3 rules balance the whole system well and there may not be another set of rules which only change the number of this one that can achieve such result that disturbs the boundary between order and chaos.

Works Cite

1. Gardner, M. (1970). The fantastic combinations of John Conway’s new solitaire game “life” (pp. 120-123). Scientific American 223.

2. Conway’s Game of Life: an Overview. (2019). Retrieved from http://edshare.soton.ac.uk/948/5/intro/gameoflife.html