Link: https://github.com/z71258847/NOC2019SPRING/tree/master/midterm
Introduction & Motivation:
In this midterm project, I implemented a polygon class and its collision detection. With this project, we can create polygon objects and interact with them in p5.js easily. The main motivation is that most objects in nature are usually polygons instead of simple ellipses or rectangles. Therefore, I think having a polygon API for p5.js will be beneficial for the following development of the final project. Due to the time limit, only convex polygons are supported in this project.
Project Description:
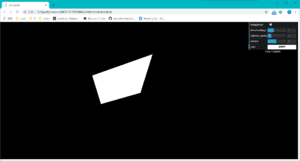
To create convex polygons, we have to first choose the vertices of the polygon. Press keyboard “A” will put a point on the mouse position to show that it is select as one of the possible vertices. Press keyboard “S” will undo the last selection. After finish selecting vertices, press keyboard “E” will automatically select the convex hull of the points to form a polygon. Note that the internal points will be ignored.
After creating several polygons, the polygons will attract each other according to the attractionMagnitude, which can be modified through the control panel to change how strong they attract each other. When they collide, they will push against each other according to the collisionCoefficient, which can be modified through the control panel to change how elastic they are when collision. The velocityLimit in the control panel to avoid an unreasonable velocity. Also, we can change the color of the next polygon by selecting the color in the control panel.
Debug Mode:
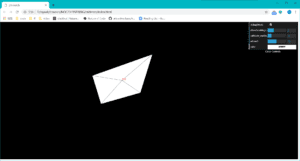
When the debug mode is on, the decomposition of the polygons will be shown by the lines between vertices and the gravity center. Also, the mass of the polygon will be shown beside the gravity center, and the mass will be proportional to the size of the polygon.
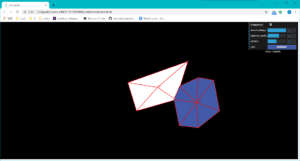
Another feature of the debug mode is that when two polygons collide, the outline of both polygons will be set to red, and therefore the collision detection can be clearly seen.
Algorithm Illustration:
Convex Hull: Graham Scan Algorithm
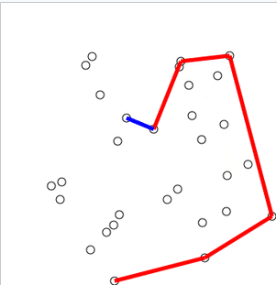
Image Reference: https://en.wikipedia.org/wiki/Graham_scan
First, we will find the bottom-most (if equal then the leftmost) point, since it will certainly be one of the vertices. Then we parse the other points in the counter-clockwise order according to the bottom-most point. This sort can be done by checking the sign of the cross products of the vector pairs (OA and OB where O is the bottom-most point). Finally, we want to pick the convex hull vertices counter-clockwise. In this procedure, only left turns can be made. Therefore, when finding a right turn, the point will not be considered as a participant of the convex hull. Again, the left turns and right turns can be determined by the sign of cross products.
Collision Detection: The Separating Axis Theorem
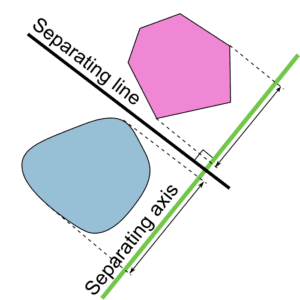
Image Reference: https://en.wikipedia.org/wiki/Hyperplane_separation_theorem
When two convex polygons don’t collide, there always exists a separating line between them, and the line perpendicular to the separating line is called the separating axis. Also, there always exists a separating line that is parallel to one of the side of the polygons.
Therefore, we can go through all the possible separating axis (all the normal vectors of the sides) to find whether two polygons collide. For each possible separating axis, we use the dot product to project all the nodes of two polygons to the separating axis. After projection, if two polygons don’t collide according to this separating axis, the set of projected nodes of polygon A (a set of value according to A) will not intersect with the set of polygon B. Finally, if it turns out that no separating axis can separate the two polygons, then they are considered as collide.
All the codes can be found in the github link above.
Further Improvements:
The weakest point of this project is that it hasn’t been applied to form an artistic or a story-telling form. Therefore, in my final project, I will focus more on improving the feeling of the audience using the techniques.
The reactions of the collision seem to be weird because the rotation during collision hasn’t been introduced. Therefore, it can be useful to study the physics of rotation when two polygons collide. Also, concave polygons can be supported using other algorithms.
Reference: