EXAMPLES
Example 1: symmetric rigidly framed structure subject to uniform loading
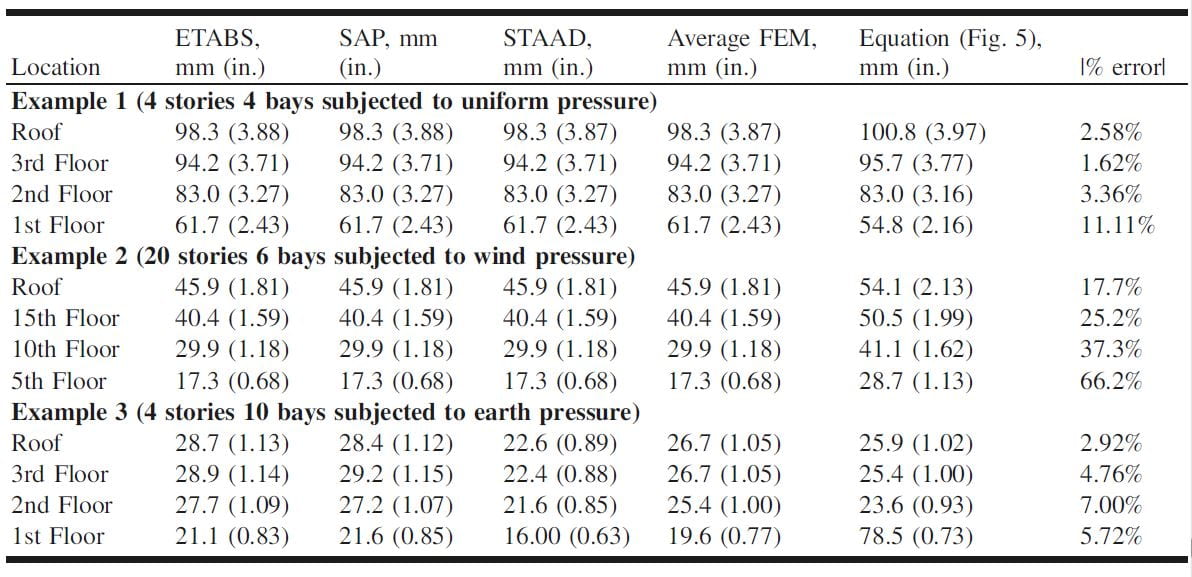
Example 1 is a 4 story, 4 bay structures subject to uniform loading, the column length and bay width are both 3 m (10 ft). Columns and beams are 0.3 m × 0.3 m (12 in. × 12 in.), and the inertia of the columns and beams are Ic = Ib = 6.75 × 10–4 m4 (0.0833 ft4). Frames are spaced 3m (10 ft) on centre. The loading is uniformly distributed with a magnitude of 12 kN/m2 (250 psf), therefore the 4-story frames are subject to a two dimensional total load, W = 445 kN (100 kips).
| Loading Type | Units | Example 1, uniform | Example 2, wind or seismic | Example 3, earth |
| Maximum lateral stress | kPa (psf) | 12 (250) | 4.8 (100) | 70.85 (1480) |
| No. of bays, b | — | 4 | 6 | 10 |
| No. of stories, s | — | 4 | 20 | 4 |
| Height of column, Lc | m (ft) | 3.05 (10) | 3.05 (10) | 2.74 (9) |
| Length of beam, Lb | m (ft) | 3.05 (10) | 3.8 (12.5) | 4.57 (15) |
| Column dimensions (b×d) | mm (ft) | 300×300 (12×12) | 500×500 (20×20) | 400×400 (16×16) |
| Wall dimensions (t×d) | mm (ft) | — | — | 300×4500 (12×180) |
| Beam dimensions (b×d) | mm (ft) | 300×300 (12×12) | 400×610 (16×24) | 300×500 (12×20) |
| Inertia of column, Ic | m4 (ft4) | 6.75×10-4 (0.0833) | 5.2×10-3 (0.643) | 2.1×10-3 (0.2633) |
| Inertia of wall, Iwall | m4 (ft4) | — | — | 0.01 (1.25) |
| Inertia of beam, Ib | m4 (ft4) | 6.75×10-4 (0.0833) | 7.5×10-3 (0.888) | 3.1×10-3 (0.3858) |
| Shear Modulus, G | MPa (ksf) | 10342 (216000) | 10342 (216000) | 10342 (216000) |
| Frame spacing | m (ft) | 3 (10) | 3.8 (12.5) | 4.5 (15) |
Table 1. Parameters used in examples.
Example 2: high rise building subject to wind load
Example 2 is a 20 story, 6 bay structures subject to wind loading. The number of stories exceeds the maximum number of stories used to derive the expressions, but the example is presented to illustrate errors that can take place if the expressions are applied to tall structures having height to width less than 5. The dimensions of the structure are shown in Table 5. Wind loading is applied linearly varying from 4.8 kN/m2 (100 psf) at the top to 0 kN/m2 at the bottom, resulting in a total load, W = 445 kN (100 kips). The equivalent area, Ao and the lateral drift, δ, are computed according to equation as follows:
Example 3: rigidly framed earth retaining structure subject to earth pressure
Example 3 is a 4 story, 10 bay rigidly framed earth-retaining structure. The dimensions of the structure are shown in Table 1. A retaining wall spans the width of the structure to resist earth pressure. Earth pressure loading is applied linearly varying from 70.85 kN/m2 (1480 psf) at the bottom to 0 kN/m2 at the top, resulting in a total load, W = 1780 kN (400 kips). The earth pressure corresponds to a soil density of 19.3 kN/m3 (123 pcf) and a coefficient of lateral earth pressure of 0.33.
Table 2. Comparison of deflections computed using FEM and approximate formulas.
Primary reference
Iskander, M., F. Masood, S. Parikh, A. Dimond, and W. Aboumoussa (2012) “Closed-form expressions for lateral deflection of low-rise rigidly-framed concrete structures,” Canadian J. of Civil Engineering, Vol. 39, No. 1, pp. 20-33, doi 10.1139/l11-104, NRC Research Press