ASSUMPTIONS
SIMPLIFIED EXPRESSION FOR LATERAL DEFLECTION of RFERS
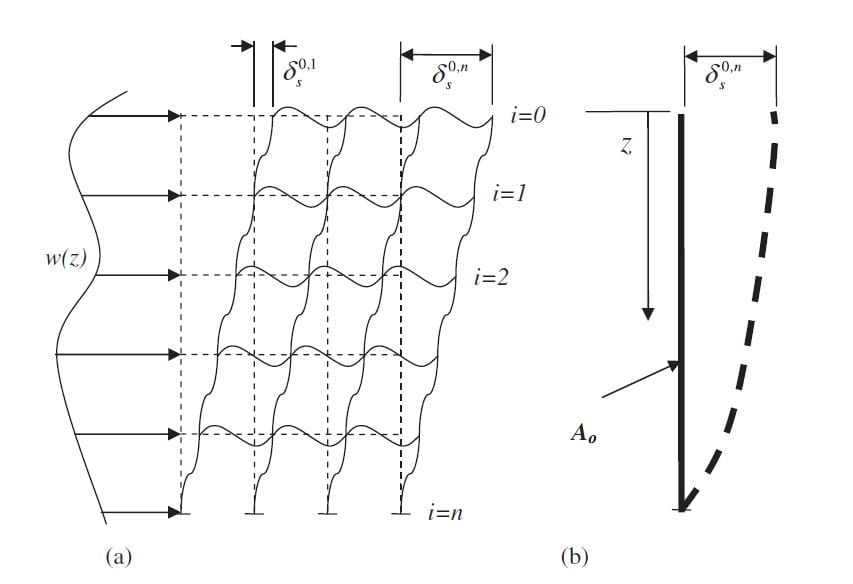
Figure 1. (a) Deflected frame and (b) equivalent cantilever beam for frame analysis
In RFERS, the lateral deflection of one floor relative to the floor below (storey drift) due to lateral earth pressure results from a combination of shear and bending deformation of the beams and columns, as shown in Figure 1(a). The fundamental premise of this work is that RFERS can be represented by an equivalent cantilever beam (Figure 3(b)), having an equivalent area, Ao, to derive an analytical expression for the deflection, γs . Bending moment causes the greatest deflection in a long beams (length>depth). Shear forces cause the greatest deflection in short beams (depth>length). A beam is considered short when the span-to-depth ratio is less than 3–8, depending on the construction material. The simplified expression is derived for RFERS having a height-to-length ratio less than 5, and may therefore be represented as short beams. Therefore, bending deflections can be neglected under transverse loads and the error caused by this approximation is calibrated using FEM.
Many RFERS are designed using a repeating fixed beam and column configuration. We stipulate that the lateral deflection for these RFERS, at any elevation, is dependent on ten variables: (1) modulus of elasticity, E; (2) Poisson’s ratio, ν; (3) total acting force, W; (4) moment of inertia of the individual columns, Ic; (5) moment of inertia of the individual beams, Ib; (6) the height of the columns, lc; (7) the length of the beams, lb; (8) the total number of stories, s; (7) the total number of bays, b; and (8) the storey from the top where the deflection is desired, i .
Primary reference
Iskander, M., A. Dimond, W. Aboumoussa, and F. Masood (2012). Approximate deflection of rigidly framed earth retaining structures due to an unknown earth pressure distribution. International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 36, pp. 517–532, doi: 10.1002/nag.1025, Wiley [link]