General Circulation of the Atmosphere

While our day-to-day experience would make us believe that weather  is a random phenomena, the atmosphere exhibits some broad structure. For instance, atmospheric scientists often distinguish between the deep tropics, characterized by heavy precipitation; the dry  subtropics, where most of the Earth’s deserts are located; the midlatitudes, home of the stromtracks; and the polar regions. This structure also corresponds to a specific wind patterns that is referred to as the ‘General Circulation of the Atmosphere’. Explains these patterns has been the object of scientific research since the 17th Century. Ed Lorenz [1,2] wrote an excellent review of the history and evolution of the theoretical understanding of the General Circulation, which I will mostly summarize here before discussing my own work.

Since the Renaissance, European sailors have been keenly aware that the tropical regions were dominated by easterly winds, also known as the Trade Winds. Edmund Halley (1686) was the first to proposes a scientific theory to explain these winds, but his explanation did not survive the test of time.  George Hadley [3] is credited with the first modern theory for the Trade Winds. His explanation relies on two keys ideas:

1. Air in the equatorial regions is lighter than at the Poles, and therefore must rise. Mass conservation implies that air at low level must flow toward the Equator, while air at high latitude must flow toward the Pole.
2. Due the the Earth rotation, the air that flows toward the Equator is deflected and turns to the West (aka, it becomes easterly, as atmospheric scientists still refers to where the wind is blowing from, not where it is blowing to… We’re a conservative bunch…)

While there are quite a few holes in Hadley theory, it contains a range of remarkable insights. In particular, it already contains the three key ingredients of any modern theory for the general circulation: it is a response to the radiative forcing by the Sun, it involves a meridional circulation that transports energy, and the Earth’s rotation plays a central role.

As time went on, more observations (mostly from ships at the time) were accumulated and it became clear that Hadley’s description did not match the new data. The main revision was due to Ferrel (1856) who identified the presence of a reverse cell in the midlatitudes (and is known nowadays as the Ferrel cell). The three cells structure – the  Hadley cell in the Tropics, Ferrel cell in the midlatitudes and polar cell at high latitudes is still the most widely used today and found in most introductory textbook.

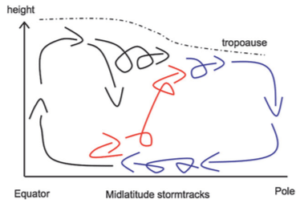
The story however did not end there. In fact, very easy in the 20th Century, it became apparent that the ‘mean’ circulation describes by the three-cell structure was wholly inadequate. The primary culprit: it did not account for the weather, or more precisely, how how weather systems move air parcels around. This idea is captured by a nice schematic representation due to Bjerknes (1921) reproduced below:

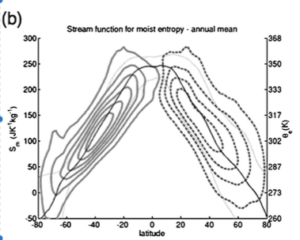
On the left side of Bjerknes’ sketch, you can see the Hadley and Ferrel cells. However, superimposed on the left-side, there are some parcel trajectories, which typically extend all the way from the equatorial regions to the polar regions. The midlatitudes are highly turbulent, with wind blowing alternatively from the equator and from the pole. Crucially, the air parcels that are coming from the equators – usually warm and moist – are not the same as the one coming from the polar regions – typically colder and drier. Under such circumstances, the ‘mean velocity’ can be quite different from what any individual parcels may be experiencing. 

This raises the question of how to assess the ‘mean motion’ of air parcel in a turbulent flow. A successful technique has been the used of the so-called isentropic analysis. The key idea here is to average the flow at constant value of the potential temperature instead of constant height or pressure. As potential temperature is more or or less conserved on a time scale of a few days (as long as you forget about clouds and condensation…), it does a better job at tracking the air parcels. When the circulation is averaged on potential temperature surfaces, one observe a single overturning cell in each hemisphere. 

As mentioned earlier, potential temperature is more less conserved as long as water vapor is not involved. It however increases dramatically when water condenses inside a cloud. An alternative is to use the equivalent potential temperature which take into accounts the heat content associated with the presence of water vapor. Interestingly, when one compute the isentropic circulation on surfaces of constant equivalent potential temperature, the mass transport increases by a factor 2!

Pauluis etal. (2008, 2009) explain that the differences between the meridional circulation averaged at constant pressure, potential temperature or equivalent potential can all be traced back to the transport by the midlatitudes weather systems. These systems pull air parcels across the midlatitudes. There are two poleward pathways, one in the free troposphere associated with the stirring of the eddies in the upper part of the atmosphere, and another near the Earth surface corresponding to the poleward flow of warm moist subtropical air that provides moisture for the storms.  The poleward flow is balanced by a return flow of cold, dry air near the Earth surfaces. 

 

1. Ed Lorenz, 1967: The nature and theory of the general circulation of the atmosphere. World Meteorological Organization, No. 218, TP 115, 161 pp.  [Part 1] [Part 2] [Part 3]
2. Ed Lorenz, 1983:  A history of prevailing ideas about the general circulation of the atmosphere.  Bull. Amer. Meteor. Soc., 64, 730-734.
3. George Hadley, 1735: Concerning the cause of the general trade-winds. Phil. Trans., 29, 58-62.
4. Olivier Pauluis, Arnaud  Czaja and Robert Korty, 2008: The global atmospheric circulation on moist isentropes. Science, 321, 1075-1078. Pauluis_Science_2008
5. Pauluis, Olivier, Arnaud Czaja, and Robert Korty. 2009. “The Global Atmospheric Circulation in Moist Isentropic Coordinates.” Journal of Climate 23 (11): 3077–93. https://doi.org/10.1175/2009JCLI2789.1.