Wash your hands! Wear masks! Keep social distance! And bring $R_0$ below one! (Right? Um… read on…)
As each of us frantically seeks information on the epidemics, chances are that you have met more than a few mentions of the quantity $R_0$ (“R-naught”) which the epidemiologists call the basic reproductive number. Journalists love to make a big fuss of it, so I bet that at a superficial glance you’ve felt like you’ve got everything crystal clear, but I also bet that those of you who have tried to figure out in detail what knowing $R_0$ actually implies, have walked away more confused than before. (Such is the magic of journalism: make things look simple by actually muddying the waters.)
$R_0$ is such a darling that even Hollywood started to love it. So, let me have none other than Kate Winslet explain what $R_0$ is:
Fantastic, isn’t it? In just a sentence she manages to say it all: $R_0$ is how many other people get infected, on average, by each infected individual. That’s easy to grasp…
And what’s so catchy is that anyone sees that if $R_0$ is larger than 1, then the epidemics will spread, but, if it’s less than 1, then the epidemics will shrink. So, that’s the one parameter that we absolutely need to know, right? (She says so… we need to know it!)
Sorry to rain on your parade, but… no.
The notion of $R_0$, albeit useful in some instances, is so fraught with problems and difficulties that in a situation like the current COVID-19 pandemics, framing policies in terms of $R_0$ may create more problems than it solves. I’ll discuss an alternative at the end of this post, but first, let me highlight two big questions (one of them actually asked in the clip…) that reveal the naughtiness of $R_0$:
- How do we measure $R_0$?
- What knowing $R_0$ is good for?
How do we measure $R_0$?
First things first, let me give you a precise definition of $R_0$: “the number of secondary cases one case would produce in a completely susceptible population“. This sounds the same as Hollywood’s definition, just more wonkish. And yet it has a key addiction: “in a completely susceptible population”. Susceptible is jargon to denote a person who can catch the disease. (Those who can’t catch it are either already infected, or they are immune, possibly because they’ve already been through the disease and have recovered.)
Thus, to measure directly $R_0$, we should be so good as to track down all the contagions that occur at the very beginning of an epidemics (when just about everybody is susceptible), and keep tracking until those initially infected either have died or have fully recovered. Considering that for new diseases, such as COVID-19, in the first weeks of the epidemics it is difficult even to ascertain who has the disease, it’s clear that a direct measurement would be a challenging task even in an Orwellian society ruled by a see-all, know-all Big Brother.
Ruling out direct measurement of $R_0$, how do scientist come up with the numbers that one reads in the news? The endearing answer is: by modeling the disease!
Those of you who are not asleep must have jumped on the chair: in order to know the one number that, allegedly, allows one to model an epidemics, one has to model the epidemics first! That’s right. That’s how it is done for just about any $R_0$ value that you read about.
Further below I’ll give an example using the very simple SIR model. (Where SIR stands for Susceptible-Infected-Recovered).
What knowing $R_0$ is good for?
The obvious implication of $R_0$ has already been mentioned: if $R_0$ is larger than 1 then the epidemics will spread. If it is less than 1 then the epidemics will fizzle like wet firecracker. If one can manage to estimate $R_0$ for some disease when everyone is still healthy and well, then one knows whether that particular disease is a threat for that particular society. For example, in modern societies, where each household enjoys abundant chlorinated running water and a perfectly efficient sewage system, the $R_0$ of cholera is much less than 1. If somebody catches cholera, the disease won’t spread. Now, picture a society where sewage fluids are dumped down the street, and running water is scarce and non-chlorinated. It’s safe to bet that cholera’s $R_0$ for that society is larger than one. If anyone (for whatever reason) catches the disease, it’ll spread.
Let’s go back to COVID-19. The disease is spreading. So we already know that its $R_0$ is larger than 1 (duh!). What else could we learn by knowing the exact $R_0$ value?
The answer is: in principle, $R_0$ determines how many individuals will not be touched by the disease (assuming that no changes are made along the way, such as lockdown measures, health care enhancements, social individual distancing (*), vaccines)
In order to explain that, let me describe an experiment that each of us can perform. Take a box full of items. Those could be pistachio nuts, glass beads, paper clips, or anything else, provided that each item looks pretty much like any other one. Extract one item and mark it (e.g. by putting on it a dot with a marker pen). That’s your “patient zero”. Then take two items out of the box, and mark them, too. those are the individuals that “patient zero” has infected. In this game no one dies, so by now patient zero has recovered, and is immune to the disease. Put “patient zero” back into the box. But the two infected are still around… For each of them take two items out of the box (that’s four in total). Mark them all, and put the two back into the box. Then, for each of the four, take two out of the box (that’s eight). Mark the eight, and put the four back into the box. Keep going in this fashion. You may even want to shake the box before extracting the new generation of diseased-to-be. But you’ll soon notice that, as you proceed in this game, you end up extracting from the box items that have already been marked. (Of course you are not supposed to be picking the items that you extract. Don’t look when you put your hand in the box. That has to be a completely random process.) The game stops when all the individuals that you extract have already been marked. When that happens, it means that all the infected individuals have come into contact only with individuals that were already infected, or had already recovered from the disease. The items in the box have reached the so-called herd immunity: the disease can’t spread anymore.
Now pour the content of the box on the table. Examine the items. Most likely you’ll find that several items have not been marked. Those are lucky individuals that, by pure chance, have managed to avoid being infected! Herd immunity has protected them.
In this game the value of $R_0$ was 2 (two extracted items for each marked item). If you had extracted three items for each marked item, that’d be $R_0=3$. Fractional $R_0$ are a little more difficult to achieve in this game, because you need to change the number of extracted items at each iteration, while maintaining a constant average (fractional) number of extracted items.
But, at this stage, it should be clear that $R_0$ determines how many people remain untouched. (If we’re talking about a zombie apocalypse, that’s the number of people who remain human, and don’t turn into zombie. Although, in a zombie apocalypse the value of $R_0$ really is likely to be infinite, so that everyone eventually turns into a zombie. Figuring why it is so is left as an exercise for the reader.)
In real world, things are a little more complicated than in the box game. For example, some people die, and only some recover and gain immunity. Infected people can’t infect others before some incubation period has elapsed, the social network is not completely random: an infected individual is more likely to infect his/her immediate family, friends, coworkers, acquaintances (in decreasing order of likelihood) rather than Mr. J. Random Guy, while in the box game (if you shake well the box at every turn, and don’t look at what you pick) every item has the same likelihood of being picked as any other item in the box.
Anyhow, if you can compute $R_0$ before an epidemics even happens (and, because of all the complications that I have just mentioned, that requires a heck of a good model) then you know how many individuals will be left untouched by the epidemics. Which sounds a moot quantity at first sight. But, in fact, it is not! If you happen to have a vaccine against that disease, then you know exactly how many people you should vaccine in order to shun the disease: as many as those who would end up being infected…
The SIR model
I’ll show how $R_0$ comes about in a simple model of epidemics. The exposition should be accessible to anyone who has taken a calculus class. But if math worries you, just skip this section.
In the SIR model one divides the population in three large categories: the susceptible ($\mathcal{S}$) , the infected ($\mathcal{I}$), and those who have recovered ($\mathcal{R}$). In this idealization no one dies, and everyone eventually recovers. The disease is spread by those who are infected. Those who have recovered are assumed to be immune, and can’t be infected again. The poor susceptible, instead, can (and will) become infected if they “get into contact” with any of the infected. What “get into contact” exactly means? That’s a question for a medical doctor, and the answer depends on the disease: you can’t catch hepatitis B by shaking hand with an infected individual, but you could catch warts in that way. Mathematical models try to lightheartedly forget as many details as possible (least they become unmanageable). To estimate how many susceptible have become infected during one day, the argument goes nearly always like in the following.
Let me call $\dot{\mathcal{S}}$ the rate of change in the number of susceptible (that is, how many individuals turn from susceptible to infected in a unit time), in a population counting $N$ individuals. It’s a safe bet to take this rate as proportional to the number $\mathcal{S}$ of susceptible: everything else being the same, the more susceptible individuals there are, the larger will be the number of them that will become infected. It is also very reasonable to assume that $\dot{\mathcal{S}}$ will increase with the fraction of infected population $\mathcal{I}/N$. This needs not be an exact proportionality, but in the SIR model, for simplicity, a proportionality is assumed. Finally, we observe that if either $\mathcal{I}=0$ (there are no infected) or $\mathcal{S}=0$ (there are no susceptible) it has to be $\dot{\mathcal{S}}=0$ (no one becomes infected), and this suggests that $\dot{\mathcal{S}}$ should be taken as proportional to the product of $\mathcal{S}$ and $\mathcal{I}/N$.
So we have the first equation of our model:\begin{equation}\dot{\mathcal{S}}=-\beta\frac{\mathcal{IS}}{N}.\label{eq:Sdot}\end{equation}The positive number $\beta$ is the proportionality constant, and the minus sign denotes the fact that the susceptible can only decrease. In the SIR model, all of the biological details of the transmission process are summarized by the single parameter $\beta$, which represents the spreading rate of the disease: it measures the number of “contacts” per unit time within the whole population. If for the disease being modeled a “contact” means exchanging blood, then the value of $\beta$ will be quite low. But if it means breathing the same air, then $\beta$ will certainly be much higher.
Any decrease in the the number of susceptible must correspond to an equal increase in the number of infected. Thus, we can write\begin{equation}\dot{\mathcal{I}}=\beta\frac{\mathcal{IS}}{N}.\end{equation}While this is correct, this is not the whole equation for $\dot{\mathcal{I}}$. The pool of infected individuals increases in number when a susceptible turns into an infected, but it decreases when an infected recovers. Of course, the larger is the number of those who are currently sick, the larger will be the daily number of recoveries. Thus, the second equation of the model becomes\begin{equation}\dot{\mathcal{I}}=\beta\frac{\mathcal{IS}}{N}-\frac{\mathcal{I}}{\tau}.\end{equation} where the time $\tau$ is an approximate measure of the typical duration of the disease.
Finally, everyone who is not infected anymore, goes into the ranks of the recovered, which then increases according to the equation\begin{equation}\dot{\mathcal{R}}=-\frac{\mathcal{I}}{\tau}.\end{equation}This is the third and last equation of the SIR model.
These three equations, as they stand, are overcomplicated: they contain the parameters: $N$, $\beta$, $\tau$. That’s two parameters too many. We can formally eliminate $N$ by dividing all three equations by $N$ and defining the new variables $S=\mathcal{S}/N$, $I=\mathcal{I}/N$, $R=\mathcal{R}/N$. Those represent the fraction of the total population which is, respectively, susceptible, infected, and recovered.
Then we re-scale time, and we use $\tau$ as the new unit of time. That makes a factor $\tau$ pop out at the denominator under $\dot{S}$, $\dot{I}$ and $\dot{R}$. And so we can rewrite the SIR equations as
$$\begin{cases} \dot{S}&=-R_0SI\\ \dot{I}&=\hphantom{-}R_0SI – I\\ \dot{R}&=\hphantom{-}I\\ \end{cases} $$Lo, and behold! $R_0$ has appeared in the equations!
Those of you who have worked out the calculations by themselves, have realized that what I called $R_0$ is the product of $\beta$ and $\tau$. Let me repeat: in the SIR model, it is $$R_0=\beta\tau.$$Within the assumptions of the model, that makes sense: $\beta$ is the average number of contacts that an individual experiences in the unit time, and $\tau$ is the length of time during which an infected person can transmit the disease. So, if there is just a handful of infected, surrounded by susceptible individuals, this product matches the definition of $R_0$ that I gave above.
Now, if we want to use the model, we need to assign a value to $R_0$. The value of $\tau$ is relatively easy to observe. The first estimates by WHO refer to a typical recovery time of two weeks. Figuring out what the value of $\beta$ should be is next to impossible from direct observation. One would face the same difficulties mentioned above about a direct measure of $R_0$. Thus we need to fit the model to data, and estimate in this way a reasonable value of $\beta$.
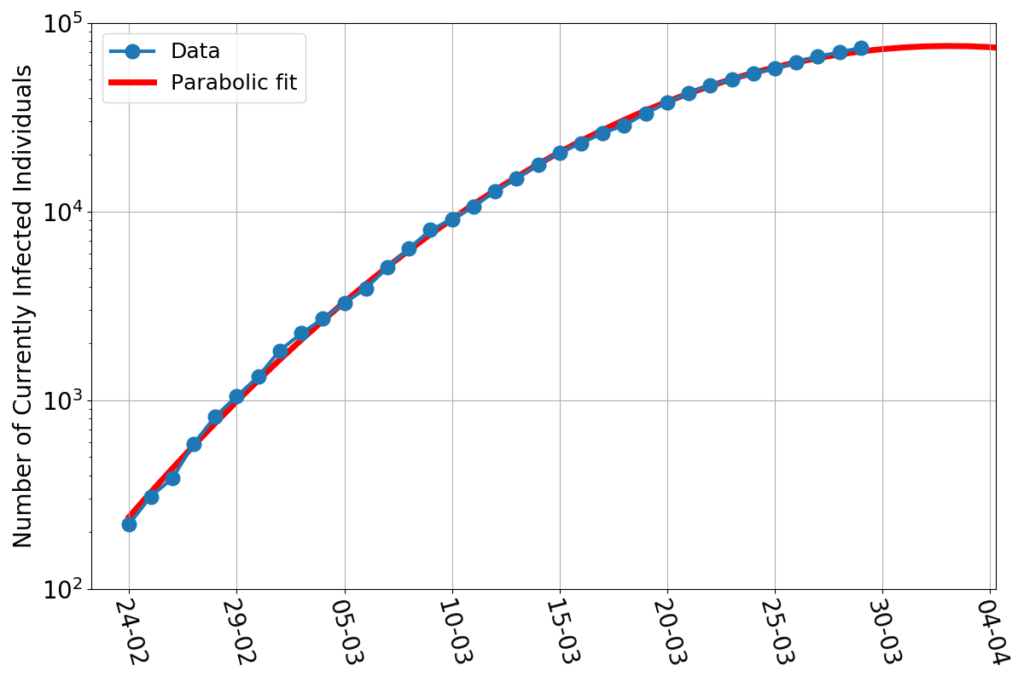
At the beginning of the epidemics nearly everyone is susceptible. Therefore, the fraction $\mathcal{S}/N\approx 1$. Hence, the equation of $\dot{\mathcal{I}}$ can be approximated to \begin{equation}\dot{\mathcal{I}}=\left(\beta-\frac{1}{\tau}\right)\mathcal{I}.\end{equation} This is easily solved (the solution is $\mathcal{I}(t)=\mathcal{I}(0)e^{\left(\beta-\frac{1}{\tau}\right)t}$), and the result can be compared with the data, seeking a suitable value of $\beta$, as in the figure below.
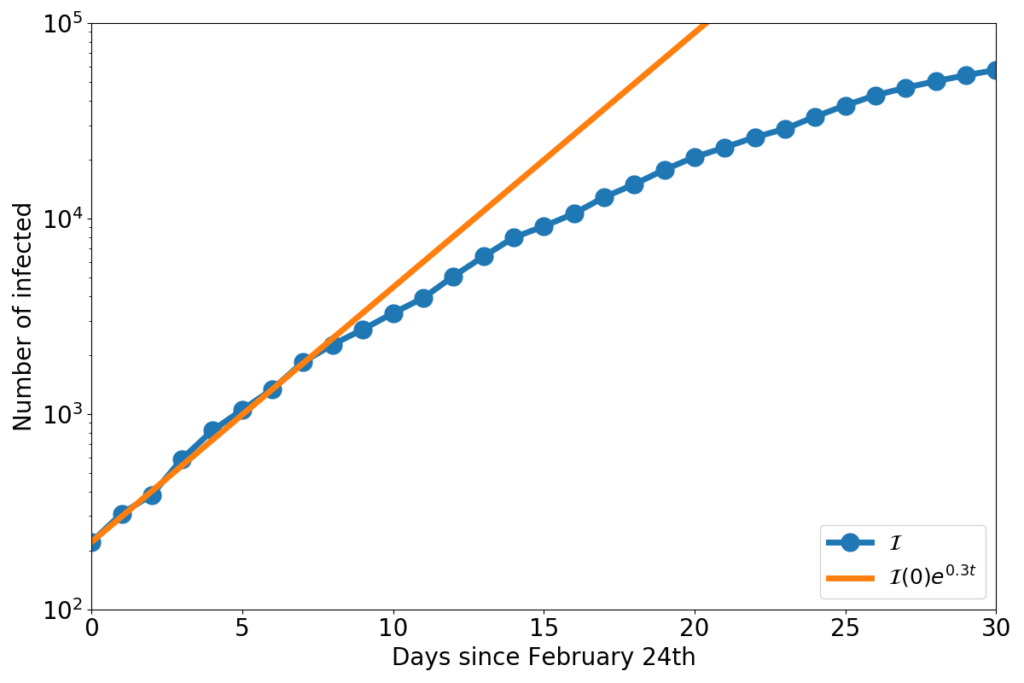
The blue dots represent the number of COVID-19 infected in Italy, and the orange line is the solution of the equation $\dot{\mathcal{I}}=(\beta-\frac{1}{\tau})\mathcal{I}$, with $\beta-\frac{1}{\tau}=0.3$.
Taking $\tau=14$ days, now we have an estimate for the COVID-19 $R_0$ in Italy:\begin{equation}R_0=\beta\tau=\left(0.3+\frac{1}{14}\right)\cdot 14 = 5.2\end{equation}
Solving the SIR equations by hand is highly non-trivial. But they’re easy to approximate numerically on a computer. The figure below shows the numerical solution that one obtains by assuming that initially one millionth of the population is infected (for Italy, that’d be 60 individuals). For the geeks, I’ve used the midpoint method, with a time step of 0.01 time units.
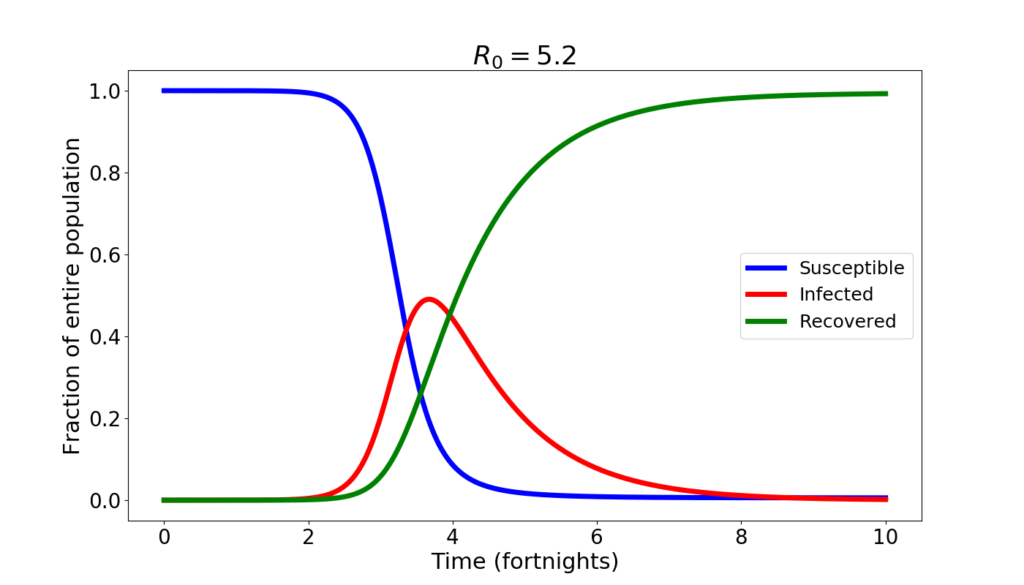
During the first month not much happens. Then, things go awry. The epidemics spreads, and by the end of the second month the infected amount to almost half of the population. After that, slowly, the epidemics subsides as the ill eventually recover and the number of susceptible that can still be infected wanes.
An epidemics like this is short. If the disease is harmful, it is also brutal. The number of those who will remain uninfected is tiny. According to the SIR model, just about 5‰ of the total population. At the peak, the situation is apocalyptic: with half of the population sick, not only the healthcare system collapses, but also the economy takes a dive worst than in a WW2 scenario. If a $R_0=5.2$ epidemics were to run unchecked, it is not exaggerated to say that human civilization would be at stakes.
So, clearly my estimate is grossly wrong! I must have made a bad mistake! After all, yes, COVID-19 is a tragedy, yes, it is making a huge damage, but human civilization is not at stakes (and the economy will take a hit, but will go seriously sour only where it’ll be mismanaged). And yet… no, no mistake. The SIR model is simple-minded, but my estimates are as good as any. If you don’t believe my little calculations, look at those made by CDC: they estimate a range for $R_0$ from 3.8 to 8.9, with a median value of 5.7. I’m squarely within CDC’s range!
Why, then, COVID-19 is not the end of human civilization? Because we are intelligent people rather than dumb animals, we change our behavior in the face of an epidemics. Thus the value of $\beta$ is not constant, but drops, even dramatically, if hygienic and lockdown measures are followed comprehensively. Here is what one would have, according to the SIR model, with $R_0=2$.
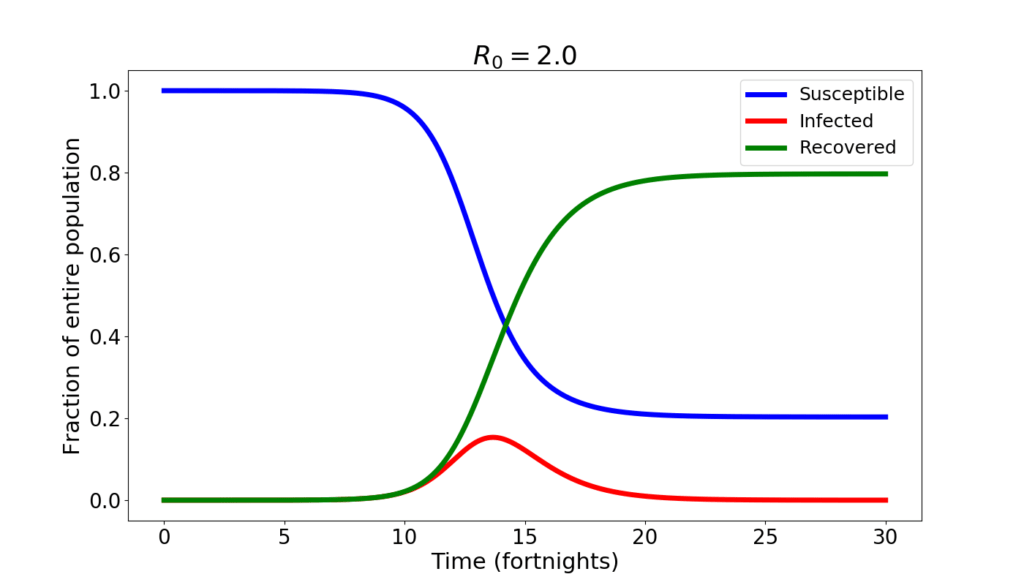
The changes are quite big. The infection peaks at 15% of the population. About 20% of the population never catches the disease. On the other hand, the peak occurs later, after about 7 months from the beginning of the epidemics, and the decline is also slower than before.
If the value of $R_0$ is further reduced to 1.2, here is what the SIR model forecasts.
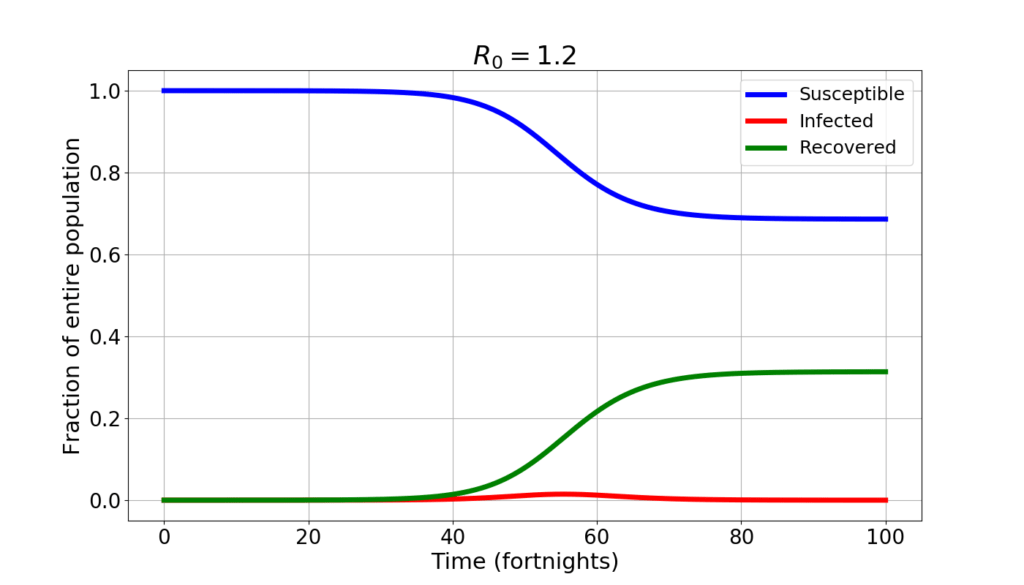
A whopping 70% of the population never catches the disease. The infected peak at 1.5% of the population. But the epidemics lasts much longer: to reach “herd immunity” (the situation where there’s enough immune people that the disease is unable to spread spontaneously) it takes well over a year.
Now you know what it is meant by “flattening the curve”: trading a higher value of $R_0$ for a lesser one lowers the peak, but makes the epidemics longer.
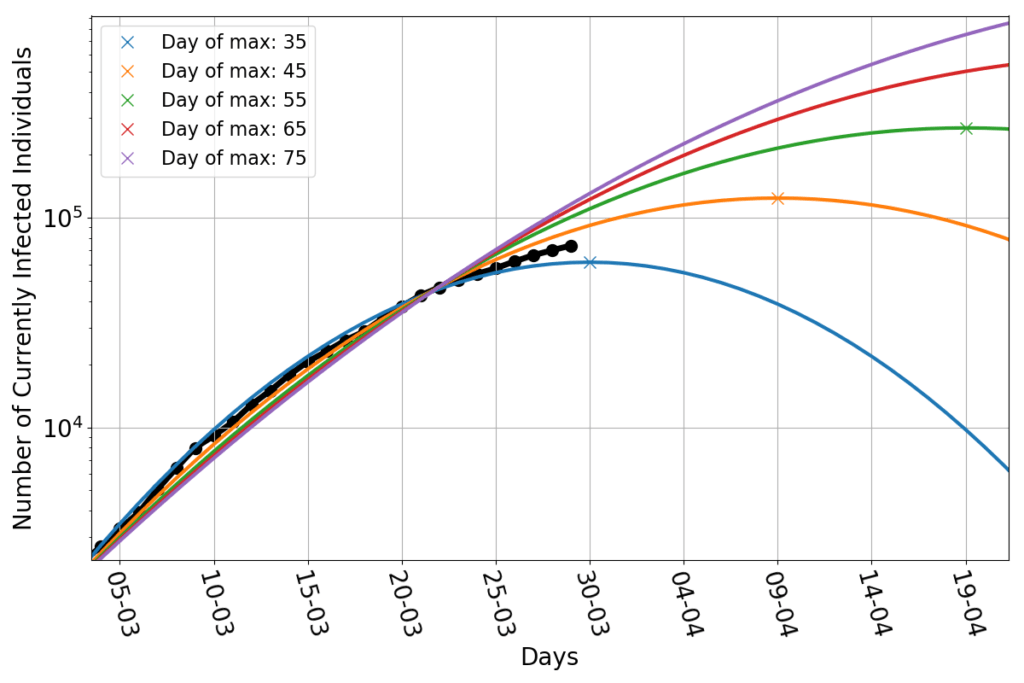
In fact, any measure that may result in lowering the contact rate is generally not taken at the beginning of the epidemics. The following graph shows the curve of the infected in four distinct simulations: initially it is $R_0=5.2$. Then after 4, 5, 6, 7 weeks, respectively the value of $R_0$ drops to 1.2, simulating a sudden and very harsh lockdown.
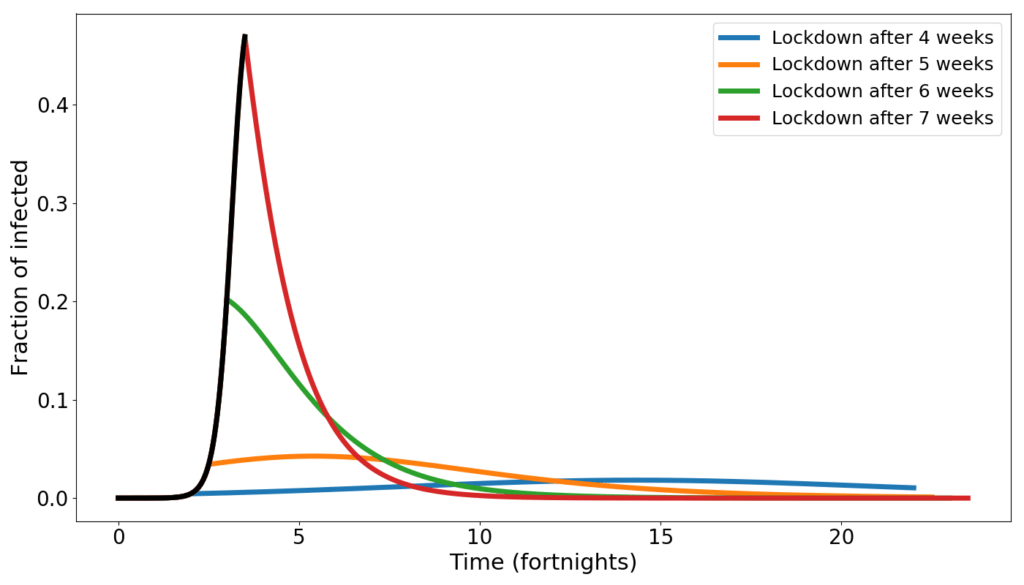
When the lockdown occurs early, the number of infected peaks late, and at low numbers. When the lockdown occurs late, the peak is early and high.
Don’t manage an epidemics by estimating $R_0$
Let’s go back to what I was saying at the beginning. Is $R_0$ a useful concept for managing an epidemics such as COVID-19?
What I have shown above is enticing: the dynamics shown by the SIR model seem to make sense, and to provide guidance. And, on a general level, it does: taking containment measures as early as possible is important for reducing the height of the peak. But at that level, the model is just reinforcing common sense.
Troubles start when one wishes to be quantitative: which value of $R_0$ will maintain the number of infected below the healthcare capacity?
I like to think that my 24 readers have, by now, got to the core of the matter. Estimating $R_0$ with a model makes all deductions that we can make with that number model-dependent. And so, if the model is inappropriate, one may risk to take very bad policy choices.
The SIR model is too simplistic for most practical uses. Not only it doesn’t distinguishes between recovered and dead, but it also doesn’t allow for an incubation period: one becomes infected (and contagious) instantly after the contact. In addition, the SIR model is completely oblivious of space. Just as in the box game, any individual has the same chance of entering in contact with an infected: the gradual geographical spreading of an epidemics is not described. Of course fixing these flaws is possible, but only at the cost of introducing new difficult-to-measure parameters.
Add to that the fact that monitoring an epidemics is far from easy. In particular for a new diseases such as COVID-19 (even testing for the virus is still a lengthy and costly process, and we are fortunate that a test was found very early in the pandemics). Some countries have even given up on carefully monitoring recoveries and deaths! Thus, hoping to reliably estimate many model parameters is a fool’s game.
A game that, unfortunately, many play. It doesn’t take much to fish out on the net sites that offer real-time estimates of $R_0$, and long-term forecasts of the epidemics.
There’s nothing wrong in making models and trying to learn from them (that’s what I do for a living…). But taking any model as a crystal ball is just plain wrong. As scientists, we should know better.
What is to be done?
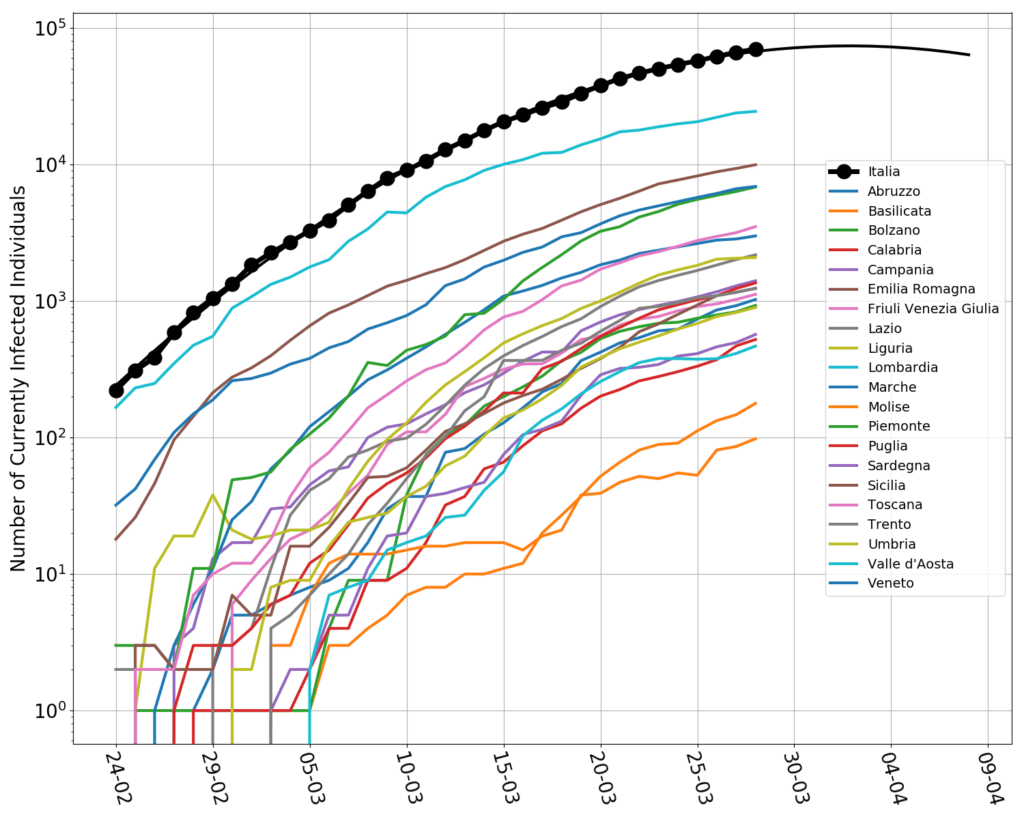
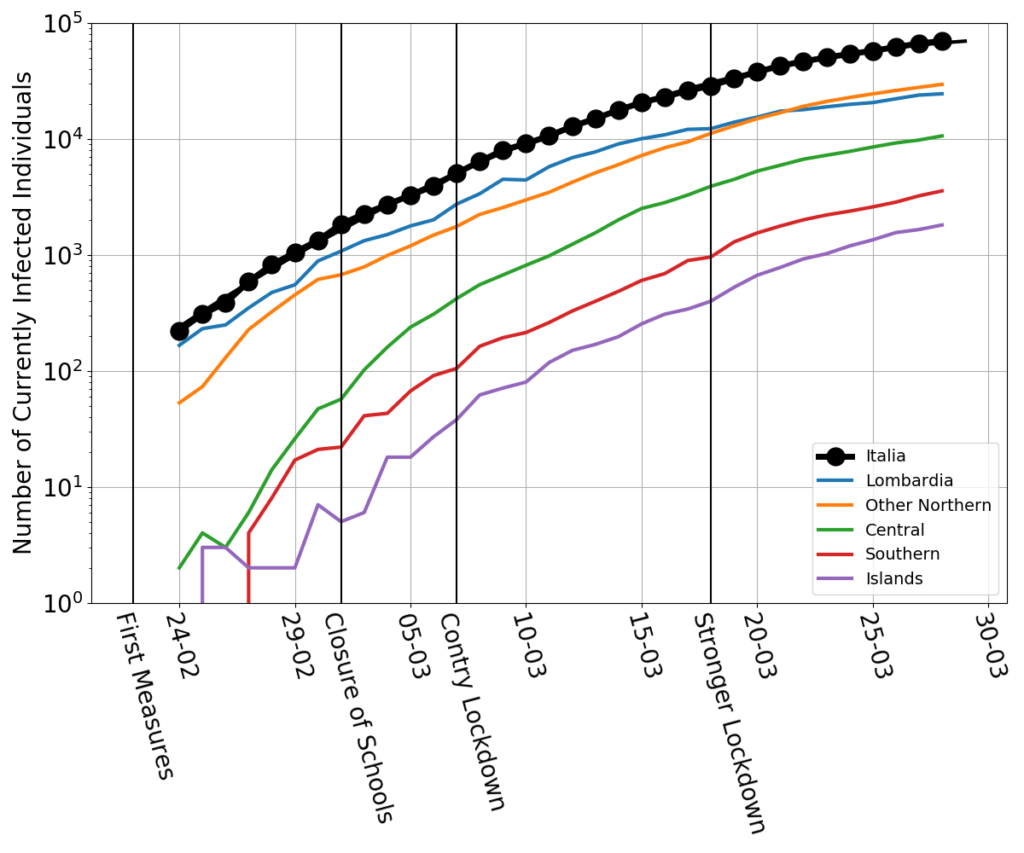
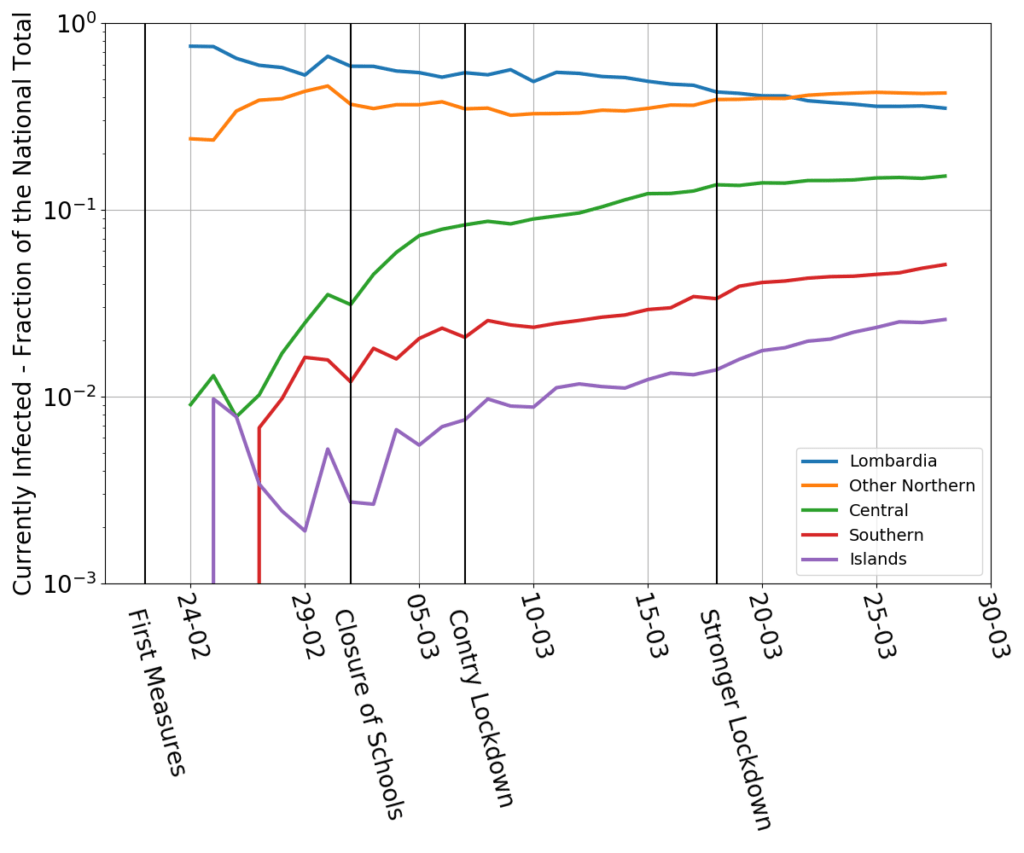
The information that really matters is the number of infected individuals present at any given moment: those are the ones who can propagate the contagion. That is what we called $\mathcal{I}$ in the SIR model, and is the difference of two quantities that need to be carefully tracked: how many individuals have caught the disease, and how many people have ceased to be diseased (either through recovery or, sadly, through death).
To gauge whether the epidemics is speeding up or slowing down, the best indicator is the growth rate $r$. That’s the ratio $\dot{\mathcal{I}}/\mathcal{I}$ and can be estimated very simply from the data, as follows $$r=\frac{\mathcal{I}_n-\mathcal{I}_{n-1}}{\mathcal{I}_n}$$ where $\mathcal{I}_n$ is the number of infected on the $n-$th day of the epidemics.
The growth rate is easy to understand if one converts it into doubling/halving times (the conversion formula is $h=(r\log_2(e))^{-1}$). Using days as a measure of time, a doubling time of, say, 5 means that the number of infected would double in 5 days (if nothing else changes in the meanwhile). A lower growth rate would translate into a higher doubling time. When yesterday’s number of infected $\mathcal{I}_{n-1}$ is higher than today’s $\mathcal{I}_n$, then one obtain a negative growth rate, and a negative doubling time, which, really, is a halving time. For example, if one finds a doubling time of -20 days, it means that, if the current growth rate doesn’t change, after 20 days the number of the infected will be half of the current one.
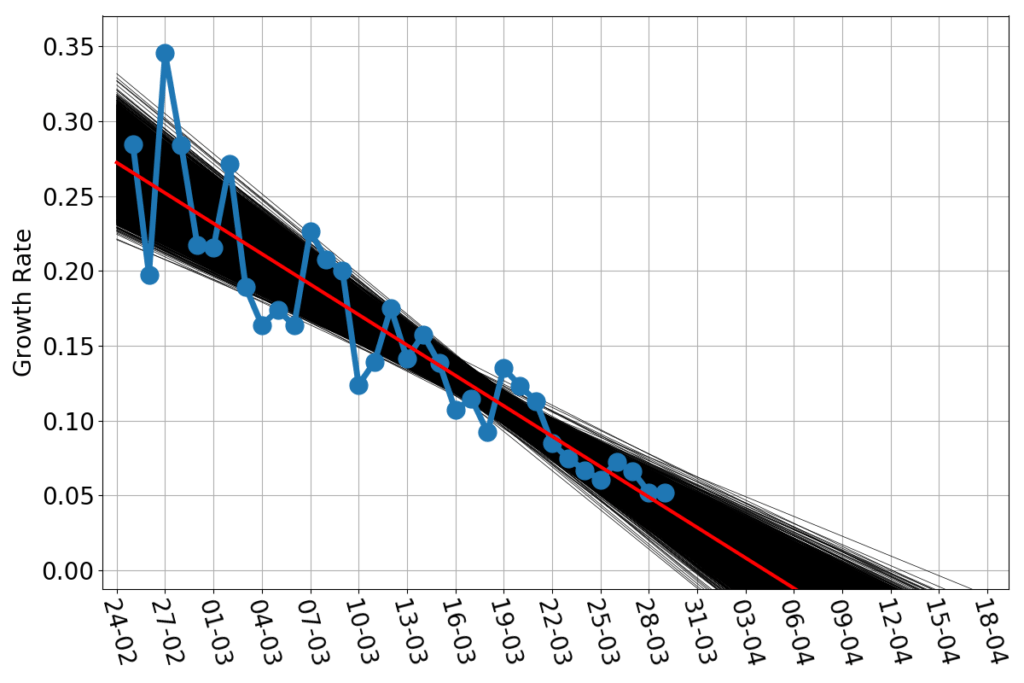
In the following graph I have plotted Italy’s growth rate (blue dots) as a function of time. The corresponding doubling/halving times are on the right-hand side axis. The red and magenta straight lines are linear trend lines, and the thin black and grey lines span the confidence interval of those trends. (See here and here for lengthier discussions of this graph).
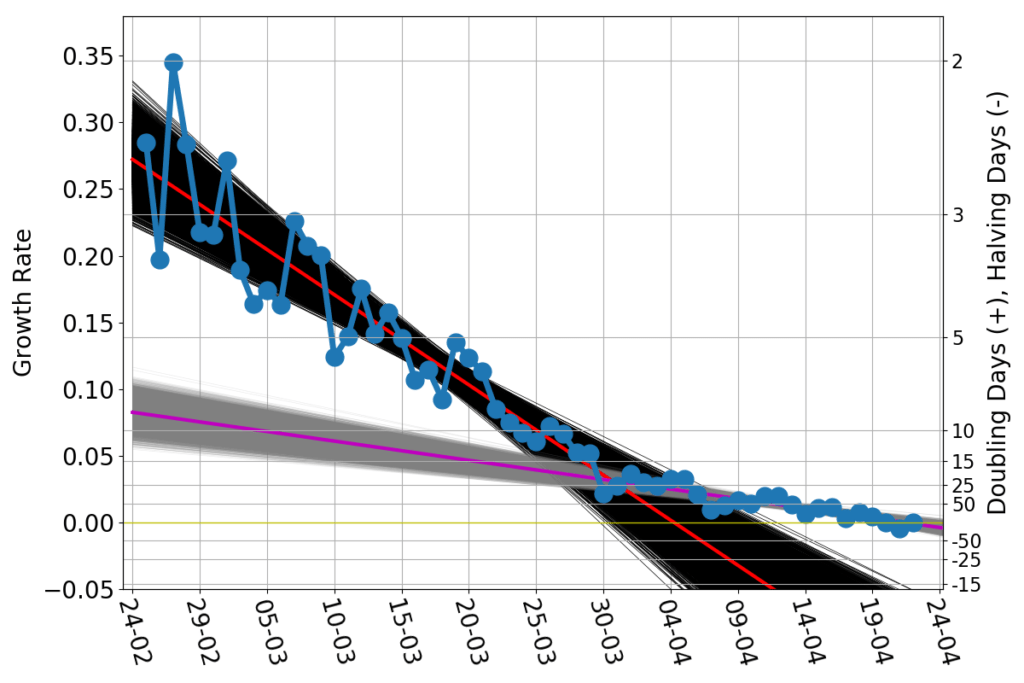
While the lockdown measures in February and March became harsher and harsher, the spread of the contagion progressed at a progressively slower rate. Once the lockdown measures could not made any harsher, the growth rate kept slowing down, but at a much lower pace. As of April 22nd, the current growth rate is about zero, suggesting that Italy has reached the peak of the number of infected.
For a policymaker, looking at the growth rate graph is alike for a sailor to looking forward, beyond the bow of the ship. One doesn’t see far, but bumps in the growth rate signal trouble just as surely as localized white caps signal dangerous shallows. Policies can (and should) be adjusted on the fly, based on what the growth rate graphs does.
Models are like maps. In the case of COVID-19 we are essentially checking the goodness of the maps by sailing into a largely unexplored territory. In this situation maps offer some general guidance, but there is no substitute for carefully looking at what lies just beyond the bow. Thus, carefully collecting data, and scrutinizing their pattern is much more important than attempting $R_0$ estimates or other vacuous exercises. Because those who rely exclusively on a map, and set the auto-pilot accordingly, are always in for some bad surprise.
____________________________________
(*) I apologize for my pedantic punctiliousness. But “social distance” is what forbids me to pat on the shoulder (or even address a word to) the V.I.P.s. That’s typically measured in dollars. The spread of a disease such as COVID-19 is reduced by maintaining a geometric (Euclidean!) distance between individuals. That’s measured in meters (or feet, if you happen to be living in some English-speaking countries).