So far we have only used arrays to graph an audio wave and we have only used the [osc~] object as an oscillator, but in this session we will use arrays to make a wavetable oscillator.
8.1 Arrays
We have learnt how to create an array (put/array), and how to modify some of its properties like its size (at creation or with right click). So let’s create an array of size 8. In the example shown in figure 8.1 I have called the array “rabbit”.
Let’s first focus on how to read from and write into arrays. On the top left there is a [tabread] object. Just as we saw with [tabwrite~] earlier, [tabread] and [tabwrite] also need to have as an argument the name of the array they are reading/writing. [tabread] receives an index number on its inlet, and outputs the value stored, while [tabwrite] needs an index in its cold inlet and value on the left inlet to write a value into that position.
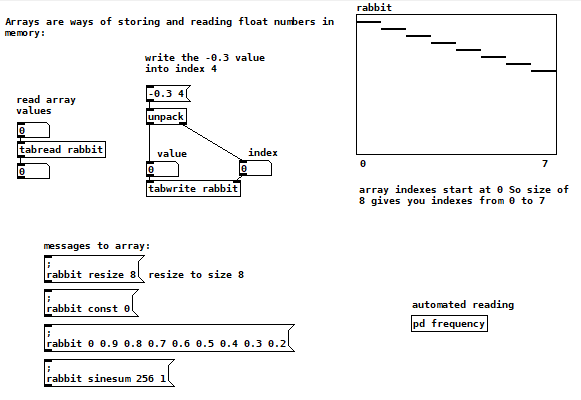
As you will notice when you try these objects, indexes in arrays start with a zero and not with a one. That means that an array with size 8, will have indexes from 0 to 7.
I have also included on the bottom left side of the patch a few semicolon messages that you can send to arrays. As you saw earlier, a semicolon (;) message works like a [send] object. So [; orange 5( will send the message “5” to a [receive orange] somewhere else. Arrays can receive semicolon messages with specific arguments. The “resize” message will change the size of your array without having to right click and change properties. The “const” message will write a constant value to all indexes in the array. You can also start with an index (in this case 0) and write the value for that index (0.9) and the values for subsequent indices (0.8 0.7 0.6 0.5 0.4 0.3 and 0.2).
Finally you can use the message sinesum to create a sum of sinewaves, by specifying the number of samples (a power of 2) and their relative amplitudes. In the message “sinesum 256 1” we are asking for a single sinewave period with amplitude 1.
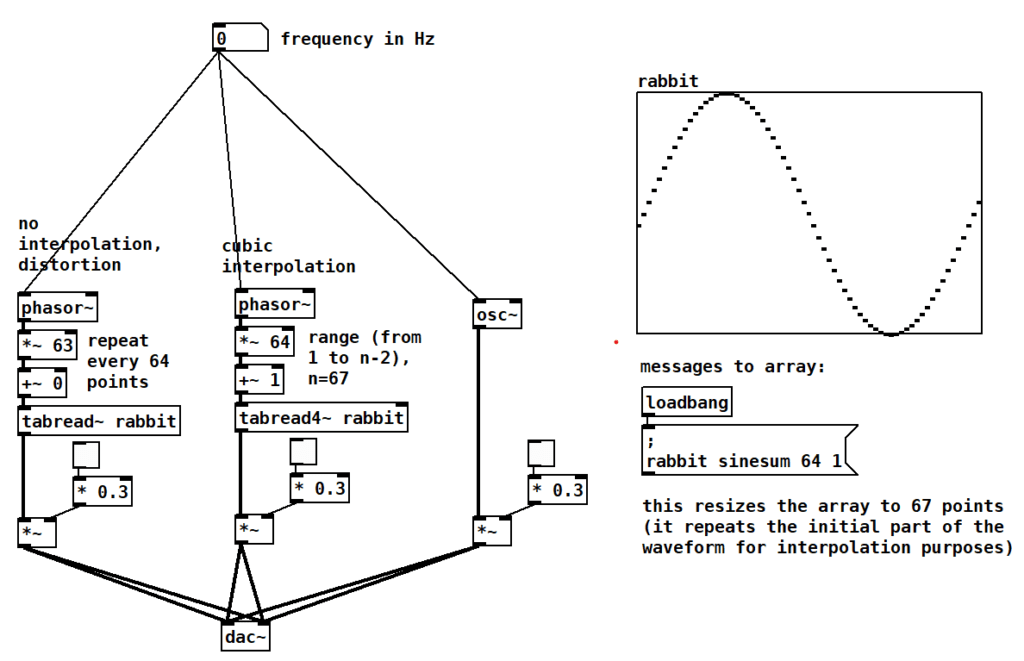
8.2 Sinewave wavetable
If you send a “sinesum 64 1” message to an array you will get a 64 point long sine wave period or cycle. (and a three extra points, but more on this later.)
To be able to read the array we send indices to [tabread] to obtain the array values as a result as we did above. However, since we are trying to generate audio, we will use [tabread~] and instead of using number boxes we will read the array with a [phasor~] object. [phasor~] produces a sawtooth wave which is equivalent to making a series of ascending line~ segments. The amplitude range of [phasor~] is 0 to 1, rather than the usual -1 to 1 we usually use in audio. Since the array has size 64, and we want phasor~ to act as the index to tabread~, we need to multiply the output of phasor~ by 64 to produce a resulting range of 0 to 64 or 0 to “array size”.
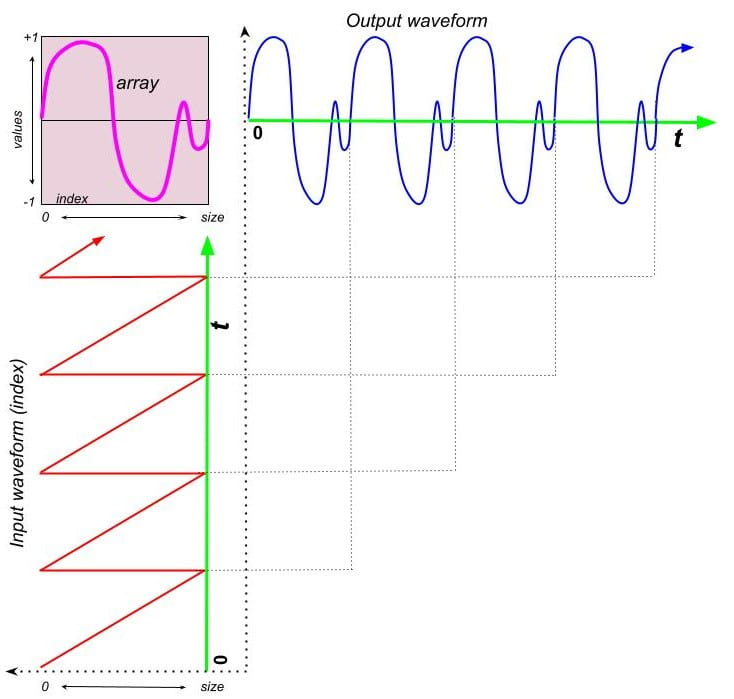
As you can see in Figure 8.3, using [phasor~] as the input index signal to [tabread~] produces a resulting output waveform that repeats the waveform that is stored in the array over and over.
In consequence, whatever soundwave is stored in an array can be used as the single period of an oscillator and we can use phashor~ to read it at any frequency. This is what we call a wavetable oscillator: an oscillator that works by repeatedly reading a table with a phasor~.
8.3 Interpolation
Earlier we talked about how in digitizing audio we sample a continuous waveform using periodic measurements taken at a “sampling rate”, thus missing information that is in between the samples we take. Indeed, any frequency above nyquist (or half the sample rate) will not be audible in our recording.
Similarly, when we read from arrays we often need to estimate the value of the underlying curve between the data points contained in the array. [tabread] and [tabread~] do not interpolate at all. the value for index 1.1 is the same for index 1 and index 1.5, thus tabread~ produces a staircase kind of wave as seen in red in Figure 8.4. As you know already, these kinds of discontinuities produce distortion and undesired harmonics. For example, compare the sound of the osc~ and phasor~/tabread~ oscillators in Figure 8.1 to hear what these distortions sound like.
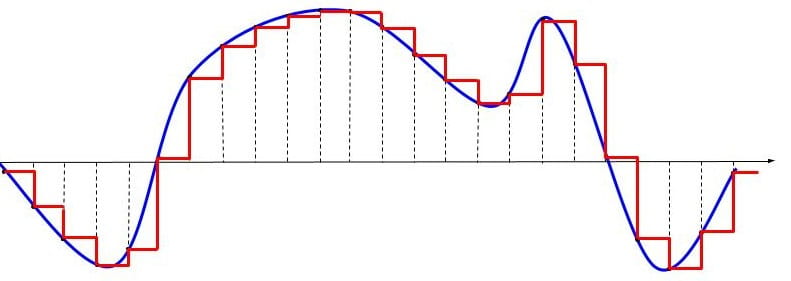
To avoid these distortions we need to do 4-point or cubic interpolation which best resembles the curvature of sine waves and which looks a little bit like the blue line above in figure 8.4. To do cubic interpolation we need to use the object tabread4~ instead of tabread~. [tabread4~] has two special requirements. Because we are doing cubic or four point interpolation, we need four samples:
- to determine the interpolated value after an index t, it needs:
- one point before t.
- two points after t.
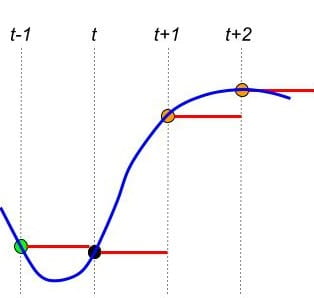
To be clear, we are trying to interpolate between points t (in black) and t-1 (in organge). So in order for the algorithm to estimate the shape of the curve in blue it needs these four points.
Thus, when we use tabread4~ we need to find the exact time of our table and then change the amplitude range of phasor~ (0 to 1) to be (1 to size-2). This construction will always look like the one in Figure 8.6.
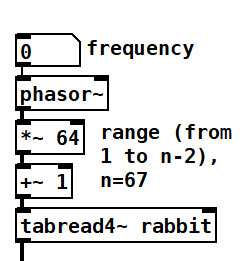
In Figures 8.2 and 8.6 you may notice that the array size is 67. Indeed when you send the message “sinesum 64 1” to an array it will create a 64 point period, but will resize the array to 67; adding 3 more points than you requested. These three points are the extra point at the beginning and the two extra points at the end.
Now you can go ahead to the patch in 8.2 and compare the phasor/tabread4~ and osc~ oscillators and see if you can hear any distortions. They should sound the same.
8.4 Wavetable Oscillators
There are several ways to produce some of the classic electronic music waveforms (square, sawtooth, triangle, etc.) or any waveform really. One way to do this is by storing a period of each of these waveforms and then making a wavetable oscillator.
To store waveforms you can:
- draw on the array by clicking and dragging.
- send a message with the values you want stored, or
- send a number n to the object [until] to produce n consecutive bangs, which you can use to drive a counter and feed that to a tabwrite. (Don’t send a bang to the object “until” unless you know what you are doing… (& check out the objects “moses” and “abs”)).